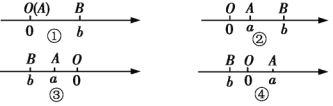
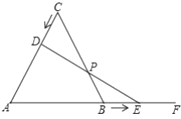
题目内容
【题目】如图,在□ABCD中,以点A为圆心,以任意长为半径画圆弧,分别交边AD、AB于点M、N,再分别以点M、N为圆心,以大于![]() 长为半径画圆弧,两弧交于点P,作射线AP交边CD于点E,过点E作EF∥AD交AB于点F.若AB=5,CE=2,则四边形ADEF的周长为______.
长为半径画圆弧,两弧交于点P,作射线AP交边CD于点E,过点E作EF∥AD交AB于点F.若AB=5,CE=2,则四边形ADEF的周长为______.

【答案】12
【解析】
首先判定四边形ADEF是平行四边形,然后根据角平分线的性质得出AD=DE,进而判定四边形ADEF是菱形,即可求出其周长.
∵□ABCD
∴AD∥BC,AB∥CD
∴DE∥AF,∠AED=∠BAE
∵EF∥AD
∴四边形ADEF是平行四边形
∵AE平分∠BAD
∴∠DAE=∠BAE
∴∠AED=∠DAE
∴AD=DE
∴四边形ADEF是菱形
∵AB=5,CE=2,
∴DE=CD-CE=AB-CE=5-2=3
∴四边形ADEF的周长为3×4=12
故答案为:12.

练习册系列答案
相关题目
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:

(说明:成绩80分及以上为优秀,![]() 分为良好,
分为良好,![]() 分为合格,60分以下为不合格)
分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:70707071727373737475767778
这一组的是:70707071727373737475767778
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分(单位:分) | 中位数(单位:分) | 众数(单位:分) |
甲 | 74.2 |
| 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)上表中n的值为_____.
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是___校的学生(填“甲”或“乙”),请说明理由.