题目内容
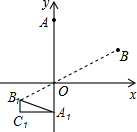（2006•福州质检）如图，直角三角形A1B1C1中，∠C1=90°，点A、A1在y轴上，且AO=2A1O，连接B1O并延长至B，使BO=2B1O，请用尺规完成下列作图：连接C1O并延长至C，使CO=2C1O，连接AB、BC、CA，则△A1B1C1∽
∽
△ABC（填≌或∽），若∠B1A1C1=30°，A1（0，-1.5），C1（-| 3 |
4
4
．分析：根据OC=2OC1，画出C点，连接即可得出三角形ABC，证△AOB∞△A1OB1，求出
=2，同理求出
=
=2即可；根据C1的坐标求出A1C1的值，根据含30度角的直角三角形性质和勾股定理求出A1B1的值，根据比例式求出即可．
| AB |
| A1B1 |
| AC |
| A1C1 |
| BC |
| B1C1 |
解答：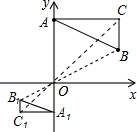
解：如图所示：△ACB是所求三角形，
∵
=
=2，∠AOB=A1OB1，
∴△AOB∽△A1OB1，
∴
=
=2，
同理：
=
=2，
=
=
=2，
∴
=
=
=2，
∴△ABC∽△A1B1C1，
∵C1（-
，-1.5），∠B1A1C1=30°，
∴A1C1=
，B1C1=1，A1B1=2，
∴AB=2A1B1=4，
故答案为：∽，4．
解：如图所示：△ACB是所求三角形，∵
| OA |
| OA1 |
| OB |
| OB1 |
∴△AOB∽△A1OB1，
∴
| AB |
| A1B1 |
| OA |
| OA1 |
同理：
| AC |
| A1C1 |
| OA |
| OA1 |
| BC |
| B1C1 |
| OC |
| OC1 |
| OA |
| OA1 |
∴
| BA |
| A1B1 |
| BC |
| B1C1 |
| AC |
| A1C1 |
∴△ABC∽△A1B1C1，
∵C1（-
| 3 |
∴A1C1=
| 3 |
∴AB=2A1B1=4，
故答案为：∽，4．
点评：本题考查了相似三角形的性质和判定，含30度角的直角三角形，勾股定理，坐标与图形性质等知识点，主要是检查学生能否熟练地运用相似三角形的性质和判定进行推理，题型较好，比较典型．难度适中．
练习册系列答案
相关题目
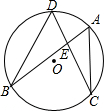（2006•福州质检）如图，⊙O中弦AB、CD相交于点E，连接BD、AC，则图中相等的角共有（ ）对．
（2006•福州质检）将一副三角尺按如图的位置摆放，则∠BOC的度数是