题目内容
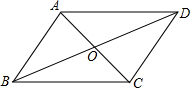 如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等
如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等
- A.1
- B.2
- C.3
- D.4
D
分析:根据SAS证△AOB≌△COD和△AOD≌△COB,根据SSS证△ABD≌△CDB和△ACD≌△CAB,即可得到答案.
解答:全等三角形有4对,如△AOD≌△COB,△AOB≌△COD,△ABD≌△CDB,△ACD≌△CAB,
理由是:在△AOB和△COD中
 ,
,
∴△AOB≌△COD,
同理△AOD≌△COB,
∴AB=CD,AD=BC,
在△ABC和△CDA中
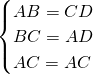 ,
,
∴△ABC≌△CDA,
同理△ADB≌△CDB,
故选D.
点评:本题考查了对全等三角形的判定定理的应用,主要培养学生运用定理进行推理的能力,此题难度不大.
分析:根据SAS证△AOB≌△COD和△AOD≌△COB,根据SSS证△ABD≌△CDB和△ACD≌△CAB,即可得到答案.
解答:全等三角形有4对,如△AOD≌△COB,△AOB≌△COD,△ABD≌△CDB,△ACD≌△CAB,
理由是:在△AOB和△COD中
 ,
,∴△AOB≌△COD,
同理△AOD≌△COB,
∴AB=CD,AD=BC,
在△ABC和△CDA中
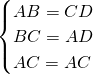 ,
,∴△ABC≌△CDA,
同理△ADB≌△CDB,
故选D.
点评:本题考查了对全等三角形的判定定理的应用,主要培养学生运用定理进行推理的能力,此题难度不大.

练习册系列答案
相关题目
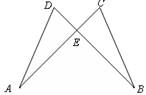
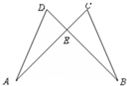 19、如图,已知AC与BD相交于点E,DE=CE,AE=BE.求证:∠A=∠B.
19、如图,已知AC与BD相交于点E,DE=CE,AE=BE.求证:∠A=∠B.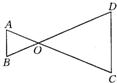 10、如图,已知AC与BD相交于点O,且AO:OC=BO:OD=2:3,AB=5,则CD=
10、如图,已知AC与BD相交于点O,且AO:OC=BO:OD=2:3,AB=5,则CD=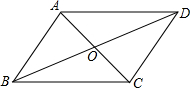 如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等( )
如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等( )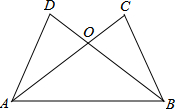 怎样探索三角形全等的条件
怎样探索三角形全等的条件