Question

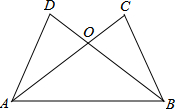
怎样探索三角形全等的条件
如图，已知AC与BD相交于点O，AD=BC，如果要得到△ACB≌△BDA，还需要补充一个条件？请你至少写出3个不同的答案，并写出每种答案中三角形全等的依据．

Answer 1

分析：添加条件AC=BD可利用SSS定理证明△ACB≌△BDA；添加条件∠DAB=∠CBA可利用SAS定理证明△ACB≌△BDA；添加条件∠D=∠C，先证明△ADO≌△BCO，再证明△ACB≌△BDA．

解答：解：添加条件AC=BD，
在△ACB和△BDA中，

AD=BC AB=AB AC=DB

，
∴△ACB≌△BDA（SSS）；
添加条件∠DAB=∠CBA，
在△ACB和△BDA中，

AD=BC ∠DAB=∠CBA AB=BA

，
∴△ACB≌△BDA（SAS）．
添加条件：∠C=∠D，
在△AOD和△BOC中，

∠AOD=∠BOC ∠D=∠C AD=BC

，
∴△AOD≌△BOC（AAS），
∴AO=BO，∠DAO=∠CBO，
∴∠OAB=∠OBA，
∴∠DAB=∠CBA，
在△DAB和△CBA中，

∠D=∠C DA=CB ∠DAB=∠CBA

，
∴△DAB≌△CBA（ASA）．

点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．