题目内容
【题目】如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于点D、E,交AB于点H,交AC于点F.P是ED延长线上一点,且PC=PF.

(1)求证:PC是⊙O的切线;
(2)若AD2=DE![]() DF,求证:CF=EF
DF,求证:CF=EF
(3)在(2)的条件下,若OH=1,AH=2,求线段PC的长.
【答案】(1)证明见解析;(2)证明见解析;(3)4![]() .
.
【解析】
试题解析:(1)连接OC,证明∠OCP=90°即可.
(2)乘积的形式通常可以转化为比例的形式,通过证明三角形相似得出.
(3)可以先根据勾股定理求出DH,再通过证明△OGA≌△OHD,得出AC=2AG=2DH,求出弦AC的长.
试题解析:(1)连接OC.

∵PC=PF,OA=OC,
∴∠PCA=∠PFC,∠OCA=∠OAC,
∵∠PFC=∠AFH,DE⊥AB,
∴∠AHF=90°,
∴∠PCO=∠PCA+∠ACO=∠AFH+∠FAH=90°,
∴PC是⊙O的切线.
(2)点D在劣弧AC中点位置时,才能使AD2=DE![]() DF,理由如下:
DF,理由如下:
连接AE.
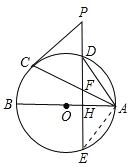
∵点D在劣弧AC中点位置,
∴∠DAF=∠DEA,
∵∠ADE=∠ADE,
∴△DAF∽△DEA,
∴AD:ED=FD:AD,
∴AD2=DE![]() DF.
DF.
(3)连接OD交AC于G.
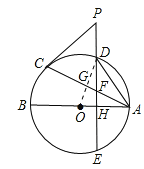
∵OH=1,AH=2,
∴OA=3,即可得OD=3,
∴DH=![]()
∵点D在劣弧AC中点位置,
∴AC⊥DO,
∴∠OGA=∠OHD=90°,
在△OGA和△OHD中,

∴△OGA≌△OHD(AAS),
∴AG=DH,
∴AC=4![]() .
.

练习册系列答案
相关题目