题目内容
 反比例函数y=
反比例函数y= (k>1)和y=
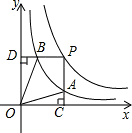
(k>1)和y= 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y= 的图象上,PC⊥x轴于C,交y=
的图象上,PC⊥x轴于C,交y= 的图象于A,PD⊥y轴于D,交y=
的图象于A,PD⊥y轴于D,交y= 的图象于B,当点P在反比例函数y=
的图象于B,当点P在反比例函数y= 上运动时,以下结论①S△ODB=
上运动时,以下结论①S△ODB= ;②四边形PAOB的面积始终不变;③PA=PB;④
;②四边形PAOB的面积始终不变;③PA=PB;④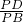 =
=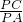 ;其中一定正确的是
;其中一定正确的是
- A.①②③
- B.①③④
- C.①②④
- D.①②
C
分析:设P(m,n),则mn=k,根据A、B两点在双曲线y= 上,且A点横坐标与P点横坐标相等,B点纵坐标与P点纵坐标相等,表示A、B两点的坐标,再对每个结论逐一判断.
上,且A点横坐标与P点横坐标相等,B点纵坐标与P点纵坐标相等,表示A、B两点的坐标,再对每个结论逐一判断.
解答:设P(m,n),则mn=k,
∵A、B两点在双曲线y= 上,
上,
∴A(m,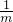 ),B(
),B( ,n),
,n),
∴①S△ODB= DB×OD=
DB×OD= ×
× ×n=
×n= ,结论正确;
,结论正确;
②S四边形PAOB=S矩形OCPD-S△OBD-S△OAC=mn- -
- =k-1(定值),结论正确;
=k-1(定值),结论正确;
③PA=n-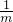 =
=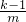 ,PB=m-
,PB=m- =
= ,PA≠PB,结论错误;
,PA≠PB,结论错误;
④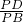 =
=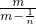 =
=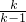 ,
,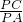 =
=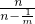 =
=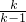 ,
,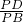 =
=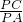 ,结论正确.
,结论正确.
故选C.
点评:本题考查了反比例函数的综合运用.关键是设P点坐标,利用点与点的坐标关系,反比例函数的性质表示相关线段的长,对每一个结论进行判断.
分析:设P(m,n),则mn=k,根据A、B两点在双曲线y=
 上,且A点横坐标与P点横坐标相等,B点纵坐标与P点纵坐标相等,表示A、B两点的坐标,再对每个结论逐一判断.
上,且A点横坐标与P点横坐标相等,B点纵坐标与P点纵坐标相等,表示A、B两点的坐标,再对每个结论逐一判断.解答:设P(m,n),则mn=k,
∵A、B两点在双曲线y=
 上,
上,∴A(m,
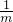 ),B(
),B( ,n),
,n),∴①S△ODB=
 DB×OD=
DB×OD= ×
× ×n=
×n= ,结论正确;
,结论正确;②S四边形PAOB=S矩形OCPD-S△OBD-S△OAC=mn-
 -
- =k-1(定值),结论正确;
=k-1(定值),结论正确;③PA=n-
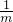 =
=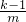 ,PB=m-
,PB=m- =
= ,PA≠PB,结论错误;
,PA≠PB,结论错误;④
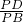 =
=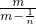 =
=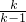 ,
,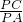 =
=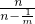 =
=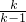 ,
,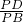 =
= ,结论正确.
,结论正确.故选C.
点评:本题考查了反比例函数的综合运用.关键是设P点坐标,利用点与点的坐标关系,反比例函数的性质表示相关线段的长,对每一个结论进行判断.

练习册系列答案
相关题目
若点(3,4)是反比例函数y=
的图象上一点,则此函数图象必经过点( )
| m2+2m+1 |
| x |
| A、(2,6) |
| B、(-2.6) |
| C、(4,-3) |
| D、(3,-4) |

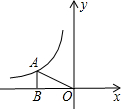 如图,点A在反比例函数y=
如图,点A在反比例函数y=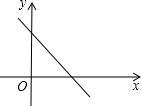 若一次函数y=kx+b的图象如图所示,则抛物线y=x2+kx+b的对称轴位于y轴的
若一次函数y=kx+b的图象如图所示,则抛物线y=x2+kx+b的对称轴位于y轴的