Question

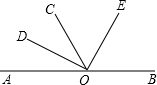
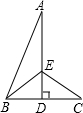
如图，点O在直线AB上，OD平分∠AOC，OE平分∠BOC，请你探索∠DOE的度数，并说明理由．若∠AOD=30°，求∠BOE的度数．

Answer 1

∠DOE=90°，理由如下：
如图，∵OD平分∠AOC，OE平分∠BOC，
∴∠COD=

1

2

∠AOC，∠COE=

1

2

∠BOC，
∴∠COD+∠COE=

1

2

（∠AOC+∠BOC）=

1

2

∠AOB，
∵∠AOB=180°，
∴∠COD+∠COE=90°，即∠DOE=90°；
当∠AOD=30°时，∠BOE=∠COE=90°-∠AOD=60°．
答：∠BOE的度数是30°．