题目内容
把两块全等的直角三角形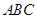 和
和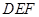 叠放在一起,使三角板
叠放在一起,使三角板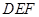 的锐角顶点
的锐角顶点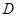 与三角板
与三角板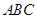 的斜边中点
的斜边中点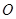 重合,其中
重合,其中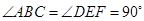 ,
,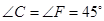 ,
,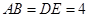 ,把三角板
,把三角板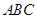 固定不动,让三角板
固定不动,让三角板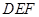 绕点
绕点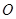 旋转,设射线
旋转,设射线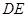 与射线
与射线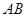 相交于点
相交于点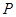 ,射线
,射线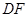 与线段
与线段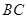 相交于点
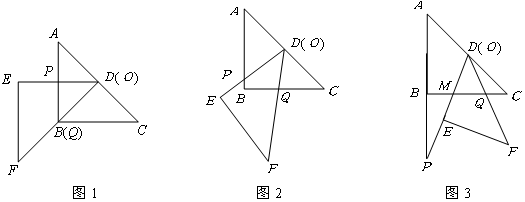
相交于点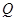 .
.
(1)如图1,当射线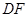 经过点
经过点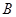 ,即点
,即点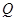 与点
与点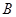 重合时,易证
重合时,易证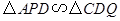 .此时,
.此时,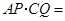 ;将三角板
;将三角板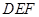 由图1所示的位置绕点
由图1所示的位置绕点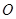 沿逆时针方向旋转,设旋转角为
沿逆时针方向旋转,设旋转角为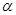 .其中
.其中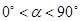 ,问
,问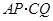 的值是否改变?答: (填“会”或“不会”);若改变,
的值是否改变?答: (填“会”或“不会”);若改变,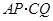 的值为 (不必说明理由);
的值为 (不必说明理由);
(2)在(1)的条件下,设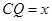 ,两块三角板重叠面积为
,两块三角板重叠面积为 ,求
,求 与
与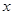 的函数关系式.(图2,图3供解题用)
的函数关系式.(图2,图3供解题用)
(1)8,不会;(2)当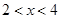 时,
时,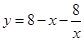
当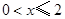 时,
时,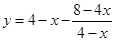
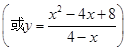 .
.
解析试题分析:(1)根据旋转的性质及相似三角形的性质求解即可;
(2)情形1:当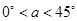 时,
时,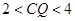 ,即
,即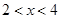 ,此时两三角板重叠部分为四边形
,此时两三角板重叠部分为四边形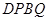 ,过
,过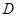 作
作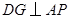 于
于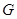 ,
,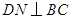 于
于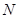 ,根据三角形的面积公式求解即可;情形2:当
,根据三角形的面积公式求解即可;情形2:当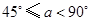 时,
时,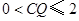 时,即
时,即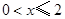 ,此时两三角板重叠部分为
,此时两三角板重叠部分为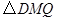 ,由于
,由于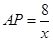 ,
,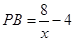 ,易证:
,易证: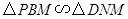 ,根据相似三角形的性质求解即可.
,根据相似三角形的性质求解即可.
(1)由题意得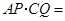 8;将三角板
8;将三角板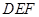 旋转后
旋转后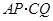 的值不会改变;
的值不会改变;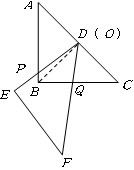
(2)情形1:当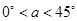 时,
时,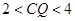 ,即
,即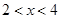 ,此时两三角板重叠部分为四边形
,此时两三角板重叠部分为四边形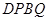 ,过
,过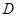 作
作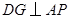 于
于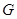 ,
,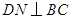 于
于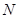 ,
,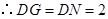
由(2)知: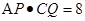 得
得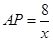
于是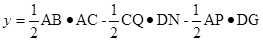
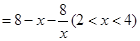
情形2:当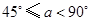 时,
时,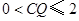 时,即
时,即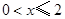 ,此时两三角板重叠部分为
,此时两三角板重叠部分为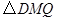 ,
,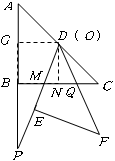
由于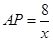 ,
,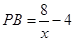 ,易证:
,易证: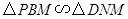 ,
,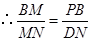 即
即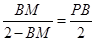 ,解得
,解得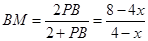
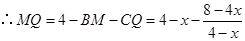
于是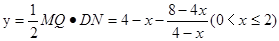
综上所述,当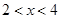 时,
时,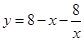
当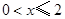 时,
时,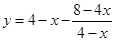
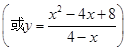 .
.
考点:旋转问题的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由. 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.

