题目内容
把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角扳ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角扳DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q。

(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD~△CDQ。此时,AP·CQ=______。
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为a.其中 0°<a<90°,问AP·CQ的值是否改变?说明你的理由。
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式。(图2,图3供解题用)
| 解:(1)8; (2)AP·CQ的值不会改变。 理由如下:在 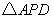 与 与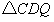 中, 中,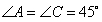 , ,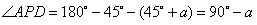 , ,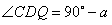 , ,即 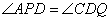 , , , ,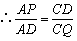 , ,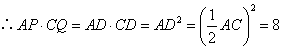 。 。 |
|
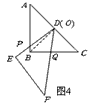
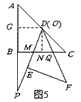
(3)情形1:如图4,当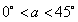 时, 时,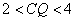 ,即 ,即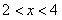 , ,此时两三角板重叠部分为四边形 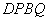 , ,过D作  于G, 于G,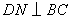 于N, 于N, 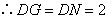 , ,由(2)知: 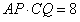 ,即 ,即 , ,于是 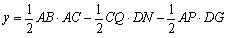 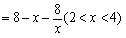 ; ;情形2:如图5,当 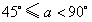 时, 时,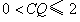 即 即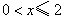 , ,此时两三角板重叠部分为 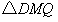 , ,由于 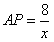 , ,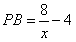 , ,易证:  , ,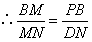 即 即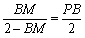 , ,解得: 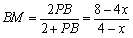 , ,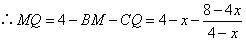 , ,于是  , ,综上所述,当 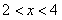 时, 时,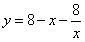 ; ;当 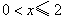 时, 时,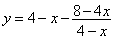 或 或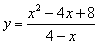 。 。 |
  |

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由. 将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
将两块斜边长度相等的等腰直角三角纸板如图(1)摆放,若把图(1)中的△BCN逆时针旋转90°,得到图(2),图(2)中除△ABC≌△CED、△BCN≌△ACF外,你还能找到一对全等的三角形吗?写出你的结论并说明理由.
