题目内容
【题目】已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;
点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s),
(1)如图(1),当x为何值时,PQ∥AB;
(2)如图(2),若PQ⊥AC,求x;
(3)如图(3),当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
【答案】
(1)解:∵∠C=60°,
∴当PC=CQ时,△PQC为等边三角形,
于是∠QPC=60°=∠B,
从而PQ∥AB,
∵PC=4﹣x,CQ=2x,
由4﹣x=2x,
解得:x= ![]() ,
,
∴当x= ![]() 时,PQ∥AB
时,PQ∥AB
(2)解:∵PQ⊥AC,∠C=60°,
∴∠QPC=30°,
∴CQ= ![]() PC,
PC,
即2x= ![]() (4﹣x),
(4﹣x),
解得:x= ![]()
(3)解:OQ=PO,理由如下:
作QH⊥AD于H,如图(3),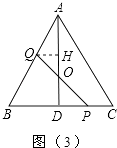
∵AD⊥BC,
∴∠QAH=30°,BD= ![]() BC=2,
BC=2,
∴QH= ![]() AQ=
AQ= ![]() (2x﹣4)=x﹣2,
(2x﹣4)=x﹣2,
∵DP=BP﹣BD=x﹣2,
∴QH=DP,
在△OQH和△OPD中,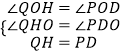 ,
,
∴△OQH≌△OPD(AAS),
∴OQ=OP.
【解析】(1)可从结论入手,若PQ∥AB,可得出△PQC为等边三角形,PC=4﹣x=CQ=2x,进而求出x;(2)利用直角三角形中30度角的性质,得出CQ= ![]() PC,求出x;(3)通过Q点作垂线,利用x的代数式表示QH=DP,构造△OQH≌△OPD,进而OQ=OP.
PC,求出x;(3)通过Q点作垂线,利用x的代数式表示QH=DP,构造△OQH≌△OPD,进而OQ=OP.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

