题目内容
【题目】已知A,C,B三地依次在一条直线上,甲骑摩托车直接从C地前往B地;乙开车以80km/h的速度从A地前往B地,在C地办理事务耽误1 h后,继续前往B地.已知两人同时出发且速度不变,又恰好同时到达B地.设出发x h后甲乙两人离C地的距离分别为y1 kmy2 km,图①中线段OD表示y1与x的函数图像,线段EF表示y2与x函数的部分图像.
(1)甲的速度为 km/h,点E坐标为 ;
(2)求线段EF所表示的y2与x之间的函数表达式;
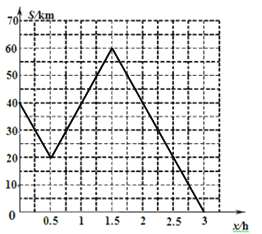
(3)设两人相距S千米,在图②所给的直角坐标系中画出S关于x的函数图像.
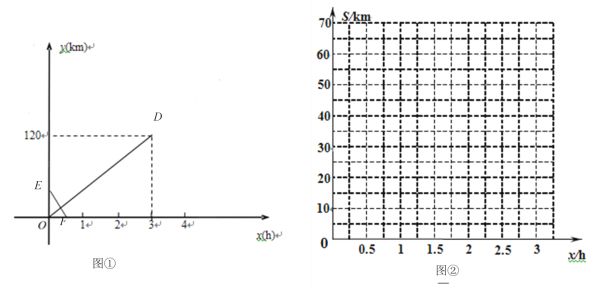
【答案】(1)40,(0,40);(2)y1=-80x+40;(3)详见解析
【解析】
(1)根据题意和图像中的数据可以直接得到甲的速度,又已知乙的速度,即可求出坐标
(2)设y2=kx+b(k≠0),函数经过F(![]() ,0) E(0,40),把两点带入即可解答
,0) E(0,40),把两点带入即可解答
(3)根据甲乙的速度和ABC三点的位置计算,即可画出
(1)由图可知甲的速度=120![]() 3=40km\h,E纵坐标=80×0.5=40,横坐标为0
3=40km\h,E纵坐标=80×0.5=40,横坐标为0
故答案为: 40,(0,40);
(2)F(![]() ,0),
,0),
设y2=kx+b(k≠0),
∵y2=k1x+b过点(0,40)(![]() ,0),
,0),
∴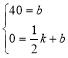 ,解得
,解得![]()
∴y1=-80x+40;
(3)

练习册系列答案
相关题目
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.