Question

【题目】如图，在△ABC中，∠ABC=∠ACB，∠A=40°，P是△ABC内一点，且∠ACP=∠PBC，则∠BPC= ．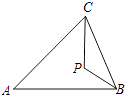

Answer 1

【答案】110°
【解析】解：∵∠BAC=40°， ∴∠ACB+∠ABC=180°﹣40°=140°，
又∵∠ACB=∠ABC，∠ACP=∠CBP，
∴∠PBA=∠PCB，
∴∠ACP+∠ABP=∠PCB+∠PBC=140°× =70°，
∴∠BPC=180°﹣70°=110°．
故答案为110°．
根据∠BAC=40°的条件，求出∠ACB+∠ABC的度数，再根据∠ACB=∠ABC，∠ACP=∠CBP，求出∠PBA=∠PCB，于是可求出∠ACP+∠ABP=∠PCB+∠PBC，然后根据三角形的内角和定理求出∠BPC的度数．