题目内容
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(1)如果点![]() 在底边
在底边![]() 上且以
上且以![]() 的速度由
的速度由![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 在腰
在腰![]() 上由
上由![]() 向
向![]() 点运动.
点运动.
①如果点![]() 与点
与点![]() 的运动速度相等,求经过多少秒后
的运动速度相等,求经过多少秒后![]() ;
;
②如果点![]() 与点
与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
(2)若点![]() 以②中的运动速度从点
以②中的运动速度从点![]() 出发,点
出发,点![]() 以
以![]() 速度从点
速度从点![]() 同时出发,都逆时针沿
同时出发,都逆时针沿![]() 三边运动,直接写出当点
三边运动,直接写出当点![]() 与点
与点![]() 第一次相遇时
第一次相遇时![]() 的运动的路程.
的运动的路程.
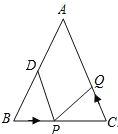
【答案】(1)①经过1秒;②![]() ;(2)160cm
;(2)160cm
【解析】
(1)①先求得BM=CN=6,MC=BD=10,然后根据等边对等角求得∠B=∠C,最后根据SAS即可证明;
②因为VM≠VN,所以BM≠CN,又∠B=∠C,要使△BMD与△CNM全等,只能BM=CM=8,根据全等得出CN=BD=10,然后根据运动速度求得运动时间,根据时间和CN的长即可求得N的运动速度;
(2)因为VN>VM,只能是点N追上点M,即点N比点M多走AB+AC的路程,据此列出方程,解这个方程即可求得.
(1)①设经过![]() 秒后
秒后![]() ,由题意可得
,由题意可得![]() ,
,
∴![]() ,
,
∴![]() ,在
,在![]() 和
和![]() 中,
中,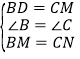 ,
,
∴![]() ,
,
∴经过1秒后![]() ;
;
设经过![]() 秒后
秒后![]() ,记
,记![]() 两点的速度分别为
两点的速度分别为![]() ,
,
∴![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
此时要使![]() 和
和![]() 全等,则
全等,则![]() ,
,
∴![]() ;
;
当![]() 时,若
时,若![]() ,则
,则![]() 中任一边长均比
中任一边长均比![]() 长,
长,
∴![]() 和
和![]() 不可能全等;
不可能全等;
若![]() ,则
,则![]() 中任一边长均比
中任一边长均比![]() 短,
短,
∴![]() 和
和![]() 不可能全等;
不可能全等;
综上所述,当![]() 时,
时,![]() .
.
(2)因为VN>VM,只能是点N追上点M,即点N比点M多走AB+AC的路程,
设经过x秒后M与N第一次相遇,
依题意得![]() x=6x+2×20,
x=6x+2×20,
解得x=![]() (秒)
(秒)
此时点M运动了![]() ×6=160(cm)
×6=160(cm)
故点![]() 与点
与点![]() 第一次相遇时点
第一次相遇时点![]() 运动路径为
运动路径为![]() .
.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案【题目】从2开始,连续的偶数相加,它们和的情况如表:
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=15=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=;
(2)如下数表是由从1开始的连续自然数组成,观察规律:
①第n行的第一个数可用含n的式子表示为;