题目内容
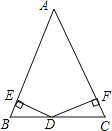
【题目】如图,在△ABC中,AB=AC,D是BC边上的一点,DE⊥AB,DF⊥AC,垂足分别为E、F,添加一个条件,使DE=DF,并说明理由.
解:需添加条件是 .
【答案】DE=DF
【解析】
试题分析:本题是开放题,应先确定选择哪对三角形,再对应三角形全等条件求解.
解:需添加的条件是:BD=CD,或BE=CF.
添加BD=CD的理由:
如图,∵AB=AC,
∴∠B=∠C.
又∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∴△BDE≌△CDF(AAS).
∴DE=DF.
添加BE=CF的理由:
如图,∵AB=AC,
∴∠B=∠C.
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD.
又∵BE=CF,
∴△BDE≌△CDF(ASA).
∴DE=DF.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<50 | a |
B | 50≤x<100 | 10 |
C | 100≤x<150 | |
D | 150≤x<200 | |
E | x≥200 |
请结合以上信息解答下列问题.

(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?