��Ŀ����
����Ŀ����֪����ͼ����Rt��ACB�У���C=90����AC=4cm��BC=3cm����P��B������BA�������A�����˶����ٶ�Ϊ1cm/s����Q��A������AC�������C�����˶����ٶ�Ϊ2cm/s������PQ�������˶���ʱ��Ϊt��s����0��t��2��������������⣺
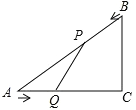
��1������AQP�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ��
��2���Ƿ����ijһʱ��t��ʹ�߶�PQǡ�ð�Rt��ACB���ܳ������ͬʱƽ�֣������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() t2+3t����2����������һʱ��t��ʹ�߶�PQ��Rt��ACB���ܳ������ͬʱƽ�֣�
t2+3t����2����������һʱ��t��ʹ�߶�PQ��Rt��ACB���ܳ������ͬʱƽ�֣�
��������
�����������1����������APQ�������Ҫ��ȷ���ױߺߵ�ֵ���ױ�AQ���Ը���Q���ٶȺ�ʱ��t��ʾ�������ؼ��Ǹߣ�������AP����A������ֵ����AP�ij�������AB��BP��ã���sinA����BC��AB��ֵ����˱�ʾ��AQ��AQ���ϵĸߺͿ��Եó�y��t�ĺ�����ϵʽ��
��2�������������ABC���ܳ������ƽ�֣���ôAP+AQ=BP+BC+CQ����ô������t��ʾ��CQ��AQ��AP��BP�ij�����ô���������ʱt��ֵ�����ǿɽ�t��ֵ���루1���������t�Ĺ�ϵʽ�У������ʱ����Ƕ��٣�Ȼ������Ƿ���������ABC�����һ�룬�Ӷ��жϳ��Ƿ������һʱ�̣�
�⣺��1������P��PH��AC��H��
�ߡ�APH�ס�ABC��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��PH=3��![]() t��
t��
��y=![]() ��AQ��PH=
��AQ��PH=![]() ��2t����3��
��2t����3��![]() t��=��
t��=��![]() t2+3t��
t2+3t��
��2�������ڣ�
���ɣ�����PQ����ABC�ܳ�ƽ�֣�
��AP+AQ=BP+BC+CQ��
����5��t��+2t=t+3+��4��2t�������t=1��
��PQ����ABC���ƽ�֣���S��APQ=![]() S��ABC����
S��ABC����![]() t2+3t=3��
t2+3t=3��
��t=1�������淽�̲�������
����������һʱ��t��ʹ�߶�PQ��Rt��ACB���ܳ������ͬʱƽ�֣�


 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�