Question

【题目】如图，在等腰△ABC中，AB=BC=4，把△ABC沿AC翻折得到△ADC．则

（1）四边形ABCD是 形；

（2）若∠B=120°，点P、E、F分别为线段AC、AD、DC上的任意1点，则PE+PF的最小值为 ．

Answer 1

【答案】（1）菱；（2）2．

【解析】

试题分析：（1）根据四边相等的四边形是菱形即可判定．即∵AB=BC，△ABC沿AC翻折得到△ADC，

∴AB=BC=AD=CD，∴四边形ABCD是菱形．

故答案为菱．

（2）作CM⊥AD交AD的延长线于M，连接PD．

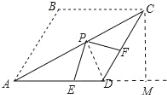
当PE⊥AD，PF⊥CD时，PE+PF最短，∵∠B=∠ADC=120°，∴∠CDM=60°，∵CD=AB=4，∠CMD=90°，

∴sin60°=，∴CM=2，∵S△ADC=S△ADP+S△CDP=ADPE+CDPF=ADCM，

∴PE+PF=CM=2，∴PE+PF的最小值为2．

故答案为2．