题目内容
在同一直角坐标系中,函数y=kx+k与y=
(k≠0)的图象大致为( )
| k |
| x |
A、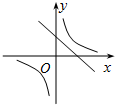 |
B、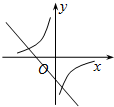 |
C、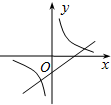 |
D、 |
分析:首先由四个图象中一次函数的图象与y轴的交点在正半轴上,确定k的取值范围,然后根据k的取值范围得出反比例函数y=
(k≠0)的图象.
| k |
| x |
解答:解:由一次函数的图象与y轴的交点在正半轴上可知k>0,故函数y=kx+k的图象过一、二、三象限,排除A,D;
又当k>0时,y=
(k≠0)的图象在二四象限,排除C.
故选B.
又当k>0时,y=
| k |
| x |
故选B.
点评:本题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
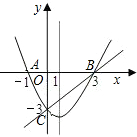 如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点.
如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点. 爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣现象,即鞋子的号码与鞋子的长(cm)之间存在着某种联系,经过收集数据,得到下表:
爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣现象,即鞋子的号码与鞋子的长(cm)之间存在着某种联系,经过收集数据,得到下表: