题目内容
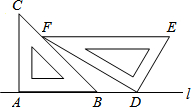 (2013•秀洲区二模)一副三角板按如图方式摆放,A、B、D三点在直线l上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠EFD=30°,已知DE=10cm,求:
(2013•秀洲区二模)一副三角板按如图方式摆放,A、B、D三点在直线l上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠EFD=30°,已知DE=10cm,求:(1)点E到直线l的距离;
(2)B、D两点间的距离.
分析:(1)过E作EG⊥l于G,过F作FH⊥l于H,求出∠GED的度数,利用三角函数的知识即可求出EG的长度;
(2)在△FBH和△FHD中,分别求出HB,HD的长度,然后用HD-HB的长度即可求得B、D两点间的距离.
(2)在△FBH和△FHD中,分别求出HB,HD的长度,然后用HD-HB的长度即可求得B、D两点间的距离.
解答:解:(1)过E作EG⊥l于G,
∵∠EFD=30°,∠EDF=90°
∴∠FED=60°,
∴∠GED=30°,
∴GE=
DE=5
cm,
∴点E到直线l的距离为5
cm;
(2)∵EF∥AD,
∴FH=EG=5
,
∵∠C=45°,
∴BH=FH=5
,
∵∠FDH=∠EFD=30°,
∴DH=
FH=15,
∴BD=15-5
,
即B、D两点间的距离为(15-5
)cm.
∵∠EFD=30°,∠EDF=90°

∴∠FED=60°,
∴∠GED=30°,
∴GE=
| ||
| 2 |
| 3 |
∴点E到直线l的距离为5
| 3 |
(2)∵EF∥AD,
∴FH=EG=5
| 3 |
∵∠C=45°,
∴BH=FH=5
| 3 |
∵∠FDH=∠EFD=30°,
∴DH=
| 3 |
∴BD=15-5
| 3 |
即B、D两点间的距离为(15-5
| 3 |
点评:本题考查了勾股定理和三角函数的知识,解答本题的关键是根据三角函数的知识在直角三角形中求出直角边的长度,难度适中.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 (2013•秀洲区二模)如图,AB是⊙O的直径,CD是⊙O的弦,若∠BAD=48°,则∠DCA的大小为( )
(2013•秀洲区二模)如图,AB是⊙O的直径,CD是⊙O的弦,若∠BAD=48°,则∠DCA的大小为( ) (2013•秀洲区二模)平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,正方形A2013B2013C2013C2012的面积为( )
(2013•秀洲区二模)平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,正方形A2013B2013C2013C2012的面积为( )