题目内容
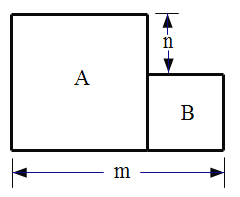
【题目】已知A、B两个边长不等的正方形纸片并排放置(如图所示)
(1)若m＝8，n＝3，则甲、乙两个正方形纸片的面积之和为: ______________
(2)用m、n表示甲、乙两个正方形纸片的面积之和为:___________________
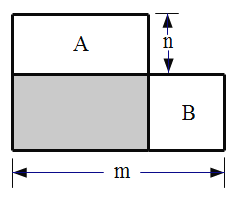
(3)若A、B两个正方形纸片的面积之和为：
，且右下图中阴影部分的面积为：
，则m=___________n=_______________________
【答案】36.5 
【解析】
（1）设A的边长为x，B的边长为y，列出等式组解得x、y的值，再根据面积公式计算即可.
（2）由题意列出m、n的关系式，根据不等式关系进行化简即可.
（3）根据题意，列出S阴影面积与A、B面积的关系式，进行化简求值即可.
(1)设A的边长为x，B的边长为y，则
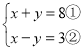
①+②得：2x=11
x=5.5
即A和B的面积之和为36.5.
（2）
解得：x=
, y=
A、B面积之和=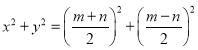 
=
(3)
=
由题意得：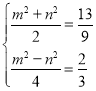
解得：
优加精卷系列答案
【题目】甲、乙两班各推选10名同学进行投篮比赛，按照比赛规则，每人各投了10个球，两个班选手的进球数统计如表，请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
（1）分别写出甲、乙两班选手进球数的平均数、中位数与众数；
（2）如果要从这两个班中选出一个班级参加学校的投篮比赛，争取夺得总进球团体的第一名，你认为应该选择哪个班？如果要争取个人进球数进入学校前三名，你认为应该选择哪个班？
【题目】甲、乙两名队员的10次射击训练，成绩分别被制成下列两个统计图.
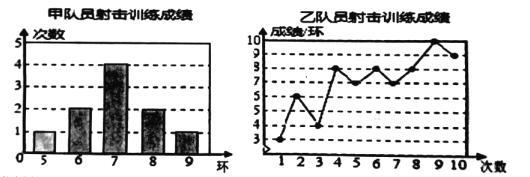
并整理分析数据如下表：
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 |
|
（1）求
，
，
的值；
（2）分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩.若选派其中一名参赛，你认为应选哪名队员？