Question

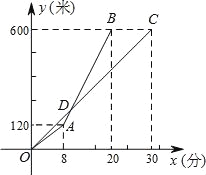
【题目】甲、乙两人沿同一路线登山，图中线段OC、折线OAB分别是甲、乙两人登山的路程y（米）与登山时间x（分）之间的函数图象．请根据图象所提供的信息，解答如下问题：

（1）求甲登山的路程与登山时间之间的函数关系式，并写出自变量x的取值范围；

（2）求乙出发后多长时间追上甲？此时乙所走的路程是多少米？

Answer 1

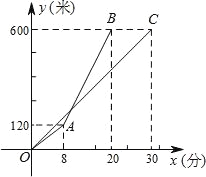
【答案】（1）y=20x（0≤x≤30）；

（2）乙出发后10分钟追上甲，此时乙所走的路程是200米．

【解析】

试题分析：（1）设甲登山的路程y与登山时间x之间的函数解析式为y=kx，根据图象得到点C的坐标，然后利用待定系数法求一次函数解析式解答；

（2）根据图形写出点A、B的坐标，再利用待定系数法求出线段AB的解析式，再与OC的解析式联立求解得到交点的坐标，即为相遇时的点．

试题解析：（1）设甲登山的路程y与登山时间x之间的函数解析式为y=kx，

∵点C（30，600）在函数y=kx的图象上，

∴600=30k，

解得k=20，

∴y=20x（0≤x≤30）；

（2）设乙在AB段登山的路程y与登山时间x之间的函数解析式为y=ax+b（8≤x≤20），

由图形可知，点A（8，120），B（20，600）

所以，，解得，所以，y=40x﹣200，

设点D为OC与AB的交点，联立，解得，

故乙出发后10分钟追上甲，此时乙所走的路程是200米．