题目内容
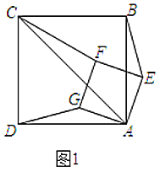
【题目】如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且DE是⊙O的切线.
(1)求证:∠CDE=![]() ∠BAC;
∠BAC;
(2)若AB=3BD,CE=4,求⊙O的半径.
【答案】(1)见解析;(2)14.
【解析】
(1)根据圆周角定理得出∠ADC=90°,按照等腰三角形的性质和已知的2倍角关系,证明∠ODE为直角即可得到答案;
(2)通过证得△CDE∽△DAE,根据相似三角形的性质即可求得.
(1)如图,连接OD,AD,
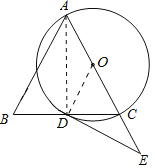
∵AC是直径,
∴∠ADC=90°,-
∴AD⊥BC,
∵AB=AC,
∴∠CAD=∠BAD=![]() ∠BAC,
∠BAC,
∵DE是⊙O的切线;
∴OD⊥DE
∴∠ODE=90°
∴∠ADC=∠ODE
∴∠CDE=∠ADO
∵OA=OD,
∴∠CAD=∠ADO,
∴∠CDE=∠CAD,
![]() ∠CAD=
∠CAD=![]() ∠BAC,
∠BAC,
∴∠CDE=![]() ∠BAC.
∠BAC.

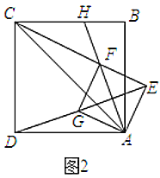
(2)解:∵AB=AC,AD⊥BC,
∴BD=CD,
∵AB=3BD,
∴AC=3DC,
设DC=x,则AC=3x,
∴AD=![]()
∵∠CDE=∠CAD,∠DEC=∠AED,
∴△CDE∽△DAE,
∴![]() ,
,
即![]()
∴DE=![]() ,x=
,x=![]() ,
,
∴AC=3x=28,
∴⊙O的半径为14.

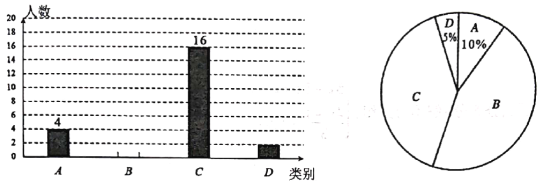
【题目】某中学八年级组织了一次“汉字听写比赛”,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,语文教研组将八年级一班和二班的成绩整理并绘制成如下的统计图,请根损换供的信息解答下列问题.
(1)把一班比赛成统计图补充完整;

(2)填表:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 85 |
二班 | 84 | 75 | c |
表格中:a=______,b=______,c=_______.
(3)请从以下给出的两个方面对这次比赛成绩的结果进行分析:
①从平均数、众数方面来比较一班和二班的成绩;
②从B级以上(包括B级)的人数方面来比较-班和二班的成绩.