题目内容
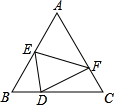 如图,E,F分别为等边△ABC的边AB,AC上的点,把△AEF沿EF折叠,点A恰好落在BC边上的点D处.已知BE=4,CF=2,设BD=x,则DC=
如图,E,F分别为等边△ABC的边AB,AC上的点,把△AEF沿EF折叠,点A恰好落在BC边上的点D处.已知BE=4,CF=2,设BD=x,则DC=分析:由折叠的性质可得出∠A=∠D=60°,再利用外角的性质∠EDC=∠B+∠BED,可得出∠BED=∠CDF,从而可判定△BED∽△CDF,利用相似三角形的对应边成比例可得出DC关于x的代数式.
解答:解:由折叠的性质可得出∠A=∠D=60°,
又∵∠EDC=∠B+∠BED(三角形外角的性质),
∴∠BED=∠CDF,
∴△BED∽△CDF,
故可得:
=
,即
=
,
解得:DC=
.
故答案为:
.
又∵∠EDC=∠B+∠BED(三角形外角的性质),
∴∠BED=∠CDF,
∴△BED∽△CDF,
故可得:
| BE |
| DC |
| BD |
| CF |
| 4 |
| DC |
| x |
| 2 |
解得:DC=
| 8 |
| x |
故答案为:
| 8 |
| x |
点评:此题考查了折叠的性质及相似三角形的判定与性质,解答本题的关键是得出△BED∽△CDF,难度一般,要注意相似三角形的对应边成比例.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图,D、E分别为等边△ABC的边AC、BC上的点,且AD=CE,BD、AE交于点N,BM⊥AE于M.求证:
如图,D、E分别为等边△ABC的边AC、BC上的点,且AD=CE,BD、AE交于点N,BM⊥AE于M.求证:
 如图,D、E分别为等边△ABC的边AC、BC上的点,且AD=CE,BD、AE交于点N,BM⊥AE于M.求证:
如图,D、E分别为等边△ABC的边AC、BC上的点,且AD=CE,BD、AE交于点N,BM⊥AE于M.求证: BN.
BN.