题目内容
 如图,D、E分别为等边△ABC的边AC、BC上的点,且AD=CE,BD、AE交于点N,BM⊥AE于M.求证:
如图,D、E分别为等边△ABC的边AC、BC上的点,且AD=CE,BD、AE交于点N,BM⊥AE于M.求证:
(1)∠CAE=∠ABD;
(2)MN= BN.
BN.
证明:(1)∵△ABC为等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠C=60°,
在△ACE和△BAD中,
 ,
,
∴△ACE≌△BAD(SAS),
∴∠CAE=∠ABD;
(2)∵△ACE≌△BAD,
∴∠EAC=∠ABD,
∴∠BNM=∠ABD+∠BAN=∠EAC+∠BAN=∠BAC=60°,
在Rt△BMN中,∠MBN=30°,
则MN= BN.
BN.
分析:(1)由三角形ABC为等边三角形,得到AB=AC=BC,∠BAC=∠ABC=∠C=60°,再由AD=CE,利用SAS得出三角形ACE与三角形BAD全等,由全等三角形的对应角相等即可得证;
(2)由(1)得出的全等得到∠EAC=∠ABD,由∠BNM为三角形ABN的外角,利用外角性质得到∠ABN为60°,在直角三角形BNM中,利用30度直角三角形的性质得到BN=2MN,即可得证.
点评:此题考查了等边三角形的性质,以及含30度直角三角形的性质,熟练掌握等边三角形的性质是解本题的关键.
∴AB=AC=BC,∠BAC=∠ABC=∠C=60°,
在△ACE和△BAD中,
 ,
,∴△ACE≌△BAD(SAS),
∴∠CAE=∠ABD;
(2)∵△ACE≌△BAD,
∴∠EAC=∠ABD,
∴∠BNM=∠ABD+∠BAN=∠EAC+∠BAN=∠BAC=60°,
在Rt△BMN中,∠MBN=30°,
则MN=
 BN.
BN.分析:(1)由三角形ABC为等边三角形,得到AB=AC=BC,∠BAC=∠ABC=∠C=60°,再由AD=CE,利用SAS得出三角形ACE与三角形BAD全等,由全等三角形的对应角相等即可得证;
(2)由(1)得出的全等得到∠EAC=∠ABD,由∠BNM为三角形ABN的外角,利用外角性质得到∠ABN为60°,在直角三角形BNM中,利用30度直角三角形的性质得到BN=2MN,即可得证.
点评:此题考查了等边三角形的性质,以及含30度直角三角形的性质,熟练掌握等边三角形的性质是解本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
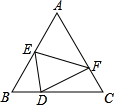 如图,E,F分别为等边△ABC的边AB,AC上的点,把△AEF沿EF折叠,点A恰好落在BC边上的点D处.已知BE=4,CF=2,设BD=x,则DC=
如图,E,F分别为等边△ABC的边AB,AC上的点,把△AEF沿EF折叠,点A恰好落在BC边上的点D处.已知BE=4,CF=2,设BD=x,则DC= 如图,D、E分别为等边△ABC的边AC、BC上的点,且AD=CE,BD、AE交于点N,BM⊥AE于M.求证:
如图,D、E分别为等边△ABC的边AC、BC上的点,且AD=CE,BD、AE交于点N,BM⊥AE于M.求证:
