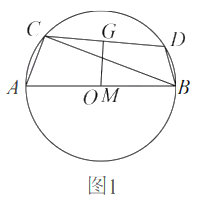题目内容
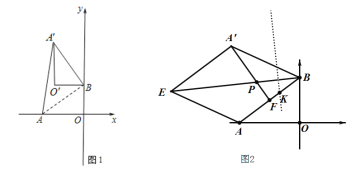
【题目】定义:我们把关于某一点成中心对称的两条抛物线叫“孪生抛物线”;(1)已知抛物线L:y=﹣x2+4与x轴交于A、B两点(A在B的左侧),与y轴交于C点,求L关于坐标原点O(0,0)的“孪生抛物线”W;(2)点N为坐标平面内一点,且△BCN是以BC为斜边的等腰直角三角形,在x轴是否存在一点M(m,0),使抛物线L关于点M的“孪生抛物线”过点N,如果存在,求出M点坐标;不存在,说明理由.
【答案】(1)y=x2﹣4;(2)存在,(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0)
,0)
【解析】
(1)根据题意画出L的图象,由W与L是“孪生抛物线”关于原点O(0,0)中心对称,则以判断W与y轴交于点(0,﹣4)且开口向上,且对称轴不变,画出W图象直接写出解析式即可;
(2)根据题意作BC的中垂线,在中垂线上找到点N,使得NB⊥NC且,NB=NC.发现这样的点N在BC的中垂线上有两个,需分情况讨论,当N在BC左侧时,设点N的坐标为(n,t),抛物线L的孪生抛物线解析式为y=(x±2m)2﹣4然后利用数形结合的思想求解即可.
解:(1)∵抛物线L与抛物线W关于原点O(0,0)成中心对称
∴W与L开口方向相反,对称轴不变,与x轴交于点(﹣2,0)和点(2,0),与y轴交于点(0,﹣4)
依题意画图象
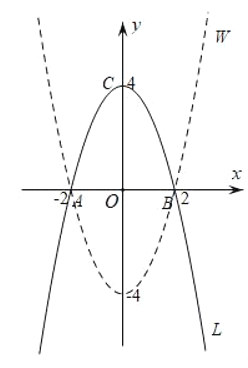
∴抛物线W的解析式为,y=x2﹣4
(2)存在.
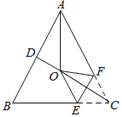
当N在BC左侧时如图2﹣1及图2﹣2
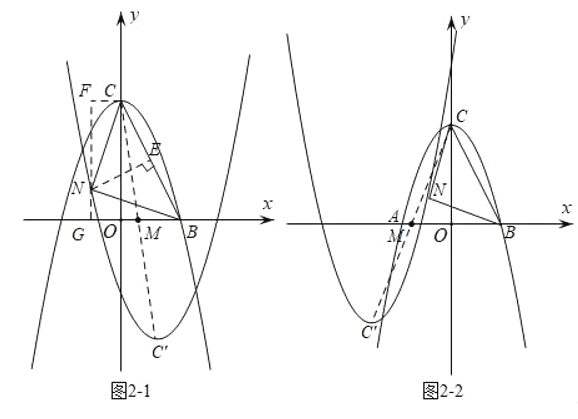
∵△BCN是以BC为斜边的等腰直角三角形
∴在BC上取其中点E并过E作线段EN⊥BC,且截取EN=![]() BC
BC
∵设L关于M(m,0)的“孪生抛物线”解析式为y=(x﹣2m)2﹣4,N(n,t).
则t=(n﹣2m)2﹣4.
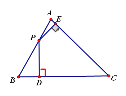
过N作线段FG⊥x轴于点G,连接CF∥x轴.
由△BCN是以BC为斜边的等腰直角三角形得BN=CN,
又∵∠FNC+∠CNB+∠BNG=180°,∠CNB=90°
∴∠FNC+∠BNG=90°
又∵∠FNV+∠NCF=90°
∴∠NCF=∠BNG
∴在△FNC与△GBN中

∴△FNC≌△GBN(AAS)
∴FN=BG=2﹣n
又∵FN=4﹣t=4﹣[(n﹣2m)2﹣4].=8﹣(n﹣2m)2
∴2﹣n=8﹣(n﹣2m)2
又∵GO=FC=NG
∴t=﹣n,即(n﹣2m)2﹣4=﹣n.
∴(n﹣2m)2=4﹣n
∴8﹣(n﹣2m)2=8﹣(4﹣n)=4+n
∴2﹣n=4+n
解得,n=﹣1
把n=﹣1代入(n﹣2m)2=4﹣n中得,(﹣1﹣2m)2=4﹣(﹣1)
解得,m=![]()
故此时M点坐标可以为,(![]() ,0),(
,0),(![]() ,0)
,0)
当N在BC右侧时如图3﹣1及3﹣2
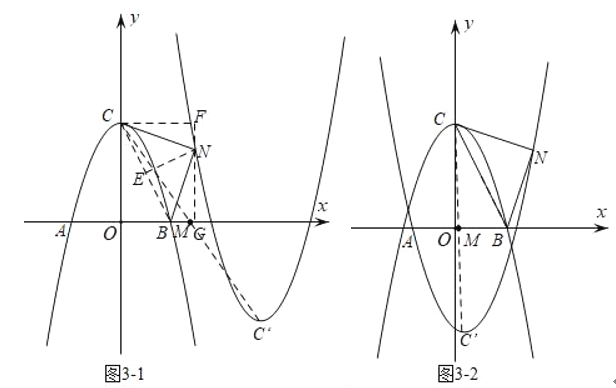
设L关于M(m,0)的“孪生抛物线”解析式为y=(x﹣2m)2﹣4,N(n,t).
同理易证△CNF≌△NBG(AAS)
∴FN=BG
即4﹣t=2﹣n
解得,t=6﹣n
∴N(n,6﹣n)
又∵△BCN为等腰直角三角形
∴BN=![]() BC=
BC=![]()
又∵在Rt△NBG中,BG2+NG2=BN2
∴(n﹣2)2+(6﹣n)2=10
整理得,n2﹣8n+15=0
解得,n=3或n=5
∴N(3,3)或N(5,1)
当N点坐标为(5,1)时,△BNC不是等腰直角三角形,这与题目已知条件相矛盾,
故N点坐标只能取(3,3).
又∵N在L的“孪生抛物线”上,
则把N(3,3)代入y=(x﹣2m)2﹣4中得,
3=(3﹣2m)2﹣4
解得,m=![]() 或m=
或m=![]()
故此时M点的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
综上所述,满足题意的M点的坐标可以为(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).