题目内容
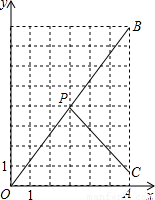
 已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.在图上画出所有线段PC,使分割得到的三角形与Rt△OAB相似,并直接写出点C的坐标.
已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.在图上画出所有线段PC,使分割得到的三角形与Rt△OAB相似,并直接写出点C的坐标.分析:根据平行于三角形一边的直线分成的三角形与原三角形相似,可得PC∥AB,PC∥OA时,分割得到的三角形与Rt△OAB相似,根据网格结构写出此时点C的坐标即可;
又当PC⊥OB时,分割得到的三角形与Rt△OAB也相似,根据网格结构,利用勾股定理求出OB的长度,然后根据相似三角形对应边成比例列式求出BC的长度,再求出AC的长度,从而得到此时点C的坐标.
又当PC⊥OB时,分割得到的三角形与Rt△OAB也相似,根据网格结构,利用勾股定理求出OB的长度,然后根据相似三角形对应边成比例列式求出BC的长度,再求出AC的长度,从而得到此时点C的坐标.
解答: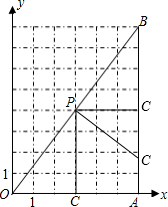 解:如图,PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0),
解:如图,PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0),
PC∥OA时,△PCB∽△OAB,此时点C的坐标为(6,4),
PC⊥OB时,△CPB∽△OAB,根据勾股定理得,OB=
=10,
∵P(3,4)为OB的中点,
∴PB=
OB=5,
∴
=
,
即
=
,
解得BC=
,
AC=AB-BC=8-
=
,
此时点C的坐标为(6,
),
综上所述,点C的坐标为(3,0),(6,4),(6,
).
 解:如图,PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0),
解:如图,PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0),PC∥OA时,△PCB∽△OAB,此时点C的坐标为(6,4),
PC⊥OB时,△CPB∽△OAB,根据勾股定理得,OB=
| 62+82 |
∵P(3,4)为OB的中点,
∴PB=
| 1 |
| 2 |
∴
| BC |
| OB |
| PB |
| AB |
即
| BC |
| 10 |
| 5 |
| 8 |
解得BC=
| 25 |
| 4 |
AC=AB-BC=8-
| 25 |
| 4 |
| 7 |
| 4 |
此时点C的坐标为(6,
| 7 |
| 4 |
综上所述,点C的坐标为(3,0),(6,4),(6,
| 7 |
| 4 |
点评:本题考查了利用相似变换作图,相似三角形的判定,需要特别注意“PC⊥OB”的情况容易漏掉而导致出错.

练习册系列答案
相关题目
 已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.
已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.