题目内容
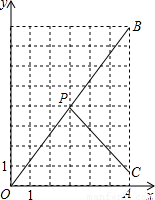
 已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.
已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.问:点C在什么位置时,分割得到的三角形与Rt△OAB相似(注:在图上画出所有符合要求的线段PC,并求出相应的点C的坐标).
分析:按照公共锐角进行分类,可以分为两种情况:当∠BOA为公共锐角时,只存在∠PCO为直角的情况;当∠B为公共锐角时,存在∠PCB和∠BPC为直角两种情况.如图,C1(3,0),C2(6,4),C3(6,
).
| 7 |
| 4 |
解答:解:过P作PC1⊥OA,垂足是C1,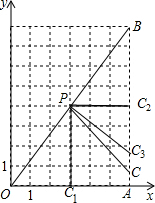
则△OC1P∽△OAB.
点C1坐标是(3,0).(2分)
过P作PC2⊥AB,垂足是C2,
则△PC2B∽△OAB.
点C2坐标是(6,4).(4分)
过P作PC3⊥OB,垂足是P(如图),
则△C3PB∽△OAB,
∴
=
.(6分)
易知OB=10,BP=5,BA=8,
∴BC3=
,AC3=8-
=
.(8分)
∴C3(6,
).(9分)
符合要求的点C有三个,其连线段分别是PC1,PC2,PC3(如图).(10分)

则△OC1P∽△OAB.
点C1坐标是(3,0).(2分)
过P作PC2⊥AB,垂足是C2,
则△PC2B∽△OAB.
点C2坐标是(6,4).(4分)
过P作PC3⊥OB,垂足是P(如图),
则△C3PB∽△OAB,
∴
| BC3 |
| BO |
| BP |
| BA |
易知OB=10,BP=5,BA=8,
∴BC3=
| 25 |
| 4 |
| 25 |
| 4 |
| 7 |
| 4 |
∴C3(6,
| 7 |
| 4 |
符合要求的点C有三个,其连线段分别是PC1,PC2,PC3(如图).(10分)
点评:本题实质上就是画直角三角形OAB的相似三角形,只不过所画的相似三角形点P已经确定了,所以就要根据网格找出三边的长,再利用对应边相似比相等,画出相似三角形.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.在图上画出所有线段PC,使分割得到的三角形与Rt△OAB相似,并直接写出点C的坐标.
已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.在图上画出所有线段PC,使分割得到的三角形与Rt△OAB相似,并直接写出点C的坐标.