题目内容
（2012•相城区一模）已知：Rt△OAB在直角坐标系中的位置如图所示，P（3，4）为OB的中点，点C为折线OAB上的动点，线段PC把Rt△OAB分割成两部分，若分割得到的三角形与Rt△OAB相似，则符合条件的C点有3
3
个．分析：按照公共锐角进行分类，可以分为两种情况：当∠BOA为公共锐角时，只存在∠PCO为直角的情况；当∠B为公共锐角时，存在∠PCB和∠BPC为直角两种情况．如图，C1（3，0），C2（6，4），C3（6，
）．
| 7 |
| 4 |
解答：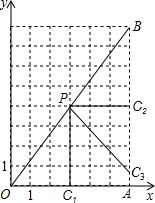
解：过P作PC1⊥OA，垂足是C1，
则△OC1P∽△OAB．
点C1坐标是（3，0）．（2分）
过P作PC2⊥AB，垂足是C2，
则△PC2B∽△OAB．
点C2坐标是（6，4）．（4分）
过P作PC3⊥OB，垂足是P（如图），
则△C3PB∽△OAB，
所以BC3：BO=BP：BA．（6分）
易知OB=10，BP=5，BA=8，
所以BC3=
，AC3=8-
=
．（8分）
所以C3（6，
）．（9分）
符合要求的点C有3个．
故答案为3．
解：过P作PC1⊥OA，垂足是C1，则△OC1P∽△OAB．
点C1坐标是（3，0）．（2分）
过P作PC2⊥AB，垂足是C2，
则△PC2B∽△OAB．
点C2坐标是（6，4）．（4分）
过P作PC3⊥OB，垂足是P（如图），
则△C3PB∽△OAB，
所以BC3：BO=BP：BA．（6分）
易知OB=10，BP=5，BA=8，
所以BC3=
| 25 |
| 4 |
| 25 |
| 4 |
| 7 |
| 4 |
所以C3（6，
| 7 |
| 4 |
符合要求的点C有3个．
故答案为3．
点评：本题考查了相似三角形的性质．此题实质上是画直角三角形OAB的相似三角形，只不过所画的相似三角形点P已经确定了，所以要根据网格找出三边的长，再利用对应边的比相等，画出相似三角形．
练习册系列答案
相关题目
（2012•相城区一模）如图，已知正比例函数和反比例函数的图象都经过点M（-2，-1），且P（-1，-2）为双曲线上的一点．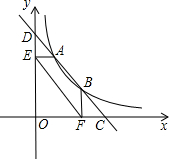
（2012•相城区一模）直线y=-2x+5分别与x轴，y轴交于点C、D，与反比例函数