Question

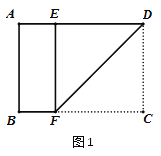
【题目】如图：在矩形ABCD中，AD=60cm，CD=120cm，E、F为AB边的三等分点，以EF为边在矩形内作等边三角形MEF，N为AB边上一点，EN=10cm；
请在矩形内找一点P，使△PMN为等边三角形（画出图形，并直接写出△PMF的面积）．

Answer 1

【答案】解：如图，以MN为边，可作等边三角形PMN；
△PMF的面积为400．（求解过程如下）．
连接PE，
∵△MEF和△PMN为等边三角形，
∴∠PMN=∠NMF=∠MFE=60°，MN=MP，NE=NF，
∴∠PME=∠NMF，
在△MPE和△MNF中，
，
∴△MPE≌△MNF（SAS），
∴∠MEP=∠MFE=60°，
∴∠PEN=60°，
∴PE∥MF，
∴S△PMF=S△MEF=EF2=400．

【解析】如图，以MN为边容易作出等边三角形，结合等边三角形的性质，连接PE，可证明△MPE≌△MNF，可证明PE∥MF，容易求得S△PMF=S△MEF ， 可求得答案．
【考点精析】通过灵活运用矩形的性质，掌握矩形的四个角都是直角，矩形的对角线相等即可以解答此题．