题目内容
【题目】定义:长宽比为![]() :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为![]() 矩形.
矩形.
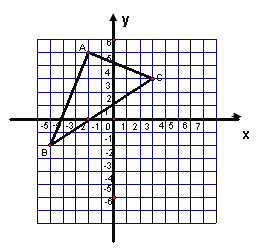
(1)如图1所示,将一张矩形纸片ABCD进行如下操作:将点C沿着过点D的直线折叠,使折叠后的点C落在边AD上的点E处,折痕为DF,通过测量发现DF=AD,则矩形ABCD是![]() 矩形吗?请说明理由.
矩形吗?请说明理由.
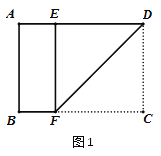
(2)我们可以通过折叠的方式折出一个![]() 矩形,如图2所示.操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.所得四边形BCEF为
矩形,如图2所示.操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.所得四边形BCEF为![]() 矩形,请说明理由.
矩形,请说明理由.
【答案】(1)矩形ABCD是![]() 矩形,理由见解析;
矩形,理由见解析;
(2)理由见解析.
【解析】试题分析:(1)根据四边形ABCD是![]() 矩形的定义,只要证明AD=
矩形的定义,只要证明AD=![]() CD即可.(2)设正方形ABCD的边长为1,求出BF的长即可解决问题.
CD即可.(2)设正方形ABCD的边长为1,求出BF的长即可解决问题.
试题解析:(1)四边形ABCD是![]() 矩形。
矩形。
理由:∵四边形ABCD是矩形,
∴∠EDC=∠DEF=∠C=90°,
∵DE=DC,
∴四边形CDEF是正方形。
∴DF=![]() DC,∵AD=DF
DC,∵AD=DF
∴AD=![]() DC,
DC,
∴矩形ABCD是2√矩形。
(2)设正方形ABCD的边长为1,则BD=![]() .
.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形。
∴∠A=∠BFE,
∴EF∥AD,
∴BGBD=BFAB,即![]() =
=![]() ,
,
∴BF=![]() ,
,
∴BC:BF=1: ![]() =
=![]() :1,
:1,
∴四边形BCEF为![]() 矩形。
矩形。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目