题目内容
【题目】如图，九（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度CD=3m，标杆与旗杆的水平距离BD=15m，人的眼睛与地面的高度EF=1.6m，人与标杆CD的水平距离DF=2m，人的眼睛E、标杆顶点C和旗杆顶点A在同一直线，求旗杆AB的高度．
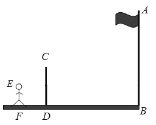
【答案】13．5米．
【解析】
试题利用三角形相似中的比例关系，首先由题目和图形可看出，求AB的长度分成了2个部分，AH和HB部分，其中HB=EF=1．6m，剩下的问题就是求AH的长度，利用△CGE∽△AHE，得出
，把相关条件代入即可求得AH=11．9，所以AB=AH+HB=AH+EF=13．5m．
试题解析：连接A、C、E，过点E作EH∥FB，交DC于点G，交AB于点H，
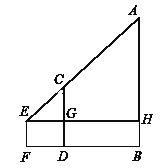
∵CD⊥FB，AB⊥FB，
∴CD∥AB
∴△CGE∽△AHE
∴
即：
∴
∴AH=11．9
∴AB=AH+HB=AH+EF=11．9+1．6=13．5（m）．
练习册系列答案
阅读快车系列答案
相关题目
【题目】已知二次函数y＝ax2＋bx＋c（a≠0），该函数y与自变量x的部分对应值如下表：
x | … | 1 | 2 | 3 | … |
y | … | 0 | ﹣1 | 0 | … |
(1)求该二次函数的表达式；
(2)不等式ax2＋bx＋c＞0的解集为 ；
不等式ax2＋bx＋c＜3的解集为 .
