题目内容
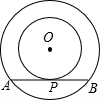如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，P为切点，如果AB=8cm，小圆半径为3cm，那么大圆半径为分析：连接OP，OA，根据切线的性质和垂径定理得到直角三角形OAP，在直角三角形中用勾股定理求出大圆的半径．
解答：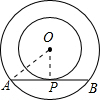
解：如图：
连接OA，OP，
∵AB是大⊙O的切线，
∴OP⊥AB，
且OP=3，AP=4，
在Rt△OAP中，OA=
=
=5．
∴大圆的半径是5cm．
故答案为：5．
解：如图：连接OA，OP，
∵AB是大⊙O的切线，
∴OP⊥AB，
且OP=3，AP=4，
在Rt△OAP中，OA=
| AP2+OP2 |
| 9+16 |
∴大圆的半径是5cm．
故答案为：5．
点评：本题考查的是切线的性质，利用切线的性质得到直角三角形，在直角三角形中用勾股定理计算求出大圆的半径．
练习册系列答案
相关题目
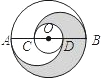如图，在以O为圆心的两个同心圆中，大圆的直径AB交小圆于C、D两点，AC=CD=DB，分别以C、D为圆心，以CD为半径作圆．若AB=6cm，则图中阴影部分的面积为
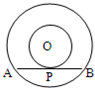9、如图，在以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P为切点，已知AB=8，大圆半径为5，则小圆半径为（ ）
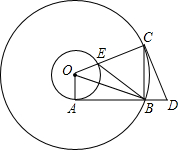（2006•静安区二模）如图，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于B，大圆的弦BC⊥AB，过点C作大圆的切线交AB的延长线于D，OC交小圆于E
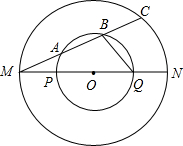如图，在以O为圆心的两个同心圆中，MN为大圆的直径，交小圆于点P、Q，大圆的弦MC交小圆于点A、B．若OM=2，OP=1，MA=AB=BC，则△MBQ的面积为
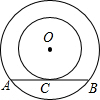如图，在以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆的半径为5cm，小圆的半径为3cm，则弦AB的长为（ ）