题目内容
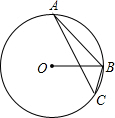 如图,△ABC内接于⊙O,∠A=15°,连接OB,则∠OBC等于
如图,△ABC内接于⊙O,∠A=15°,连接OB,则∠OBC等于
- A.30°
- B.60°
- C.65°
- D.75°
D
分析:首先连接OC,由圆周角定理,可求得∠BOC的度数,又由等腰三角形的性质,即可求得∠OBC的度数.
解答: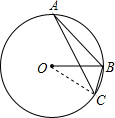 解:∵连接OC,
解:∵连接OC,
∵△ABC内接于⊙O,∠A=15°,
∴∠BOC=2∠A=30°,
∵OB=OC,
∴∠OBC=∠OCB= =75°.
=75°.
故选D.
点评:此题考查了圆周角定理与等腰三角形的性质.此题比较简单,注意掌握辅助线的作法,注意数形结合思想的应用.
分析:首先连接OC,由圆周角定理,可求得∠BOC的度数,又由等腰三角形的性质,即可求得∠OBC的度数.
解答:
 解:∵连接OC,
解:∵连接OC,∵△ABC内接于⊙O,∠A=15°,
∴∠BOC=2∠A=30°,
∵OB=OC,
∴∠OBC=∠OCB=
 =75°.
=75°.故选D.
点评:此题考查了圆周角定理与等腰三角形的性质.此题比较简单,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.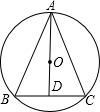 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( ) 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.