题目内容
 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.(1)判断DC是否为⊙O的切线,并说明理由;
(2)证明:△AOC≌△DBC.
分析:(1)因为C点在圆上,所以只需证明OC⊥CD即可.可先求出∠ACD=120°,∠ACO=∠A=30°,所以∠OCD=90°.得证;
(2)证明△OBC为等边三角形,运用“SSS”判定全等.
(2)证明△OBC为等边三角形,运用“SSS”判定全等.
解答: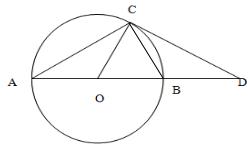 (1)解:DC是⊙O的切线.
(1)解:DC是⊙O的切线.
∵∠A=∠D=30°,
∴AC=CD,∠ACD=120°.
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠OCD=90°,
∴DC是⊙O的切线.
(2)证明:∵AB是直径,
∴∠ACB=90°,
∴∠BCD=120°-90°=30°=∠D,
∴BC=BD.
∵∠CBO=2∠D=60°,OB=OC,
∴△OBC是等边三角形,则BC=OC,
∴△AOC≌△DBC.(SSS)
 (1)解:DC是⊙O的切线.
(1)解:DC是⊙O的切线.∵∠A=∠D=30°,
∴AC=CD,∠ACD=120°.
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠OCD=90°,
∴DC是⊙O的切线.
(2)证明:∵AB是直径,
∴∠ACB=90°,
∴∠BCD=120°-90°=30°=∠D,
∴BC=BD.
∵∠CBO=2∠D=60°,OB=OC,
∴△OBC是等边三角形,则BC=OC,
∴△AOC≌△DBC.(SSS)
点评:此题考查了切线的判定、全等三角形的判定及等腰三角形的判定等知识点,难度中等.

练习册系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( ) 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.