Question

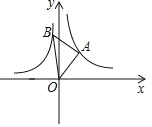
【题目】如图，在平面直角坐标系中，等腰Rt△ABO的顶点A，B分别在反比例函数y＝（k＞0）与y＝﹣ 上，且A点的横坐标为2，则k的值为（　　）

A. B. C. 1D. 1+

Answer 1

【答案】B

【解析】

作AM⊥x轴于M，作BN∥x轴，交AM于N，则BN⊥MN，易证得△AOM≌△BAN，得出AN＝OM＝2，BN＝AM，故设A（2，n），则B（2﹣n，n+2），分别代入y＝与y＝﹣，得到方程组，解方程组即可．

解：作AM⊥x轴于M，作BN∥x轴，交AM于N，则BN⊥MN，

∵△ABO是等腰直角三角形，

∴∠BAO＝90°，AB＝OA，

∴∠BAN+∠OAM＝90°，

∵∠AOM+∠OAM＝90°，

∴∠AOM＝∠BAN，

在△AOM和△BAN中

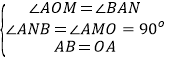
∴△AOM≌△BAN（AAS），

∴AN＝OM＝2，BN＝AM，

设A（2，n），则B（2﹣n，n+2），

∵顶点A，B分别在反比例函数y＝（k＞0）与y＝﹣上，

∴2k＝2n，

（2﹣n）（n+2）＝﹣k，

解得k＝，

故选：B．