题目内容
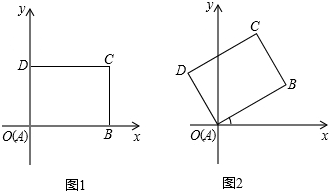
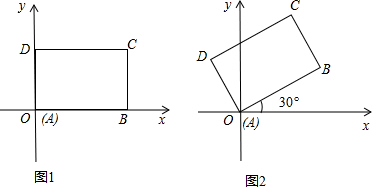
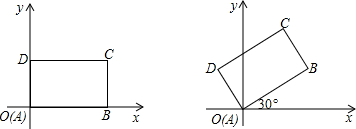
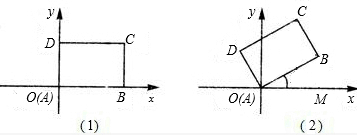
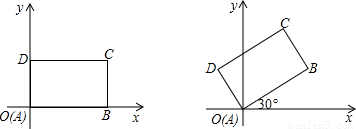
先将一矩形ABCD置于直角坐标系中,使点A与坐标系的原点重合,边AB、AD分别落在x轴、y轴上(如图1),再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图2),若AB=4,BC=3,请分别在图1和图2中求出点B和点C的坐标.
(备选数据:sin30°= ,cos30°=
,cos30°= )
)
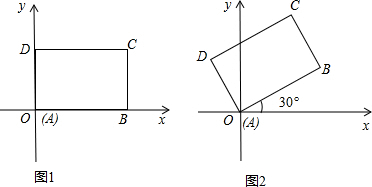
 解:在图1中,B(4,0)、C(4,3);
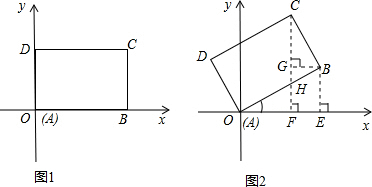
解:在图1中,B(4,0)、C(4,3);在图2中,分别过点B、C作x轴的垂线,垂足分别为E、F,过B作BG⊥CF于G,则有在Rt△ABE中,OE=ABcos30°=4×
 =2
=2 ,BE=ABsin30°=4×
,BE=ABsin30°=4× =2,
=2,∴B(2
 ,2).
,2).设AB与CF交于点H,
则由∠ABC=∠AFH,∠AHF=∠CHB,得∠BCG=∠BAE=30°,
在Rt△BGC中,BG=BCsin30°=3×
 =
=
∴OF=OE-FE=OE-BG=2
 -
- ,
,CF=CG+GF=CG+BE=
 +2=
+2=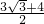 ,
,∴C点的坐标是:(2
 -
- ,
,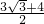 ).
).分析:在图2中分别过点B、C作x轴的垂线,垂足分别为E、F,过B作BG⊥CF于G,则有在Rt△ABE中,利用三角函数即可求得BE与OE的长面积可确定B的坐标,在直角△BCG中,利用三角函数即可求得CG,BG的长,即可求得C的坐标.
点评:本题主要考查了坐标的确定,以及三角函数,求点的坐标的问题最基本的方法是作坐标轴的垂线,转化为求线段的长的问题.

练习册系列答案
相关题目