题目内容
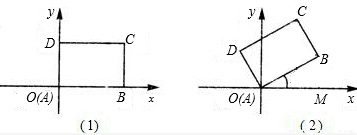
如图（1），先将一矩形ABCD置于直角坐标系中，已知AB=8，BC=6，使点A与坐标系的原点重合，边AB，AD分别落在x轴，y轴上，再将此矩形在坐标平面内按逆时针方向绕原点旋转30°，如图（2）．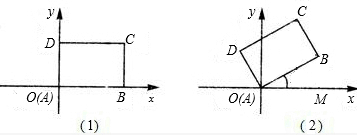
请你利用三角函数知识求出矩形ABCD旋转前后点B的坐标和点C的坐标．
分析：由题意，AB=8，AC=
=10，旋转后的B，C我们只需由各点分别向x，y轴上作垂线，求出各垂线段的长度即可．
| AB2+BC2 |
解答：解：易求得旋转前B（8，0），C（8，6）．
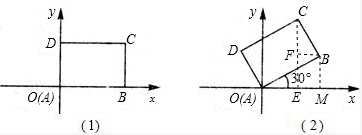
旋转后，作CE⊥x轴，垂足为E，BM⊥x轴，垂足为M，BF⊥CE垂足为F．
在Rt△ABM中，∵AB=8，∠BAM=30°
∴BM=4，AM=4
．
在Rt△CBF中，∵BC=6，∠BCF=30°
∴BF=3，CF=3
∴CE=CF+EF=3
+4，AE=AM-EM=4
-3
∴B(4
，4），C(4
-3，4+3
)．
旋转后，作CE⊥x轴，垂足为E，BM⊥x轴，垂足为M，BF⊥CE垂足为F．
在Rt△ABM中，∵AB=8，∠BAM=30°
∴BM=4，AM=4
| 3 |
在Rt△CBF中，∵BC=6，∠BCF=30°
∴BF=3，CF=3
| 3 |
∴CE=CF+EF=3
| 3 |
| 3 |
∴B(4
| 3 |
| 3 |
| 3 |
点评：着重考查学生对图形在坐标系中的旋转问题，要求学生熟练掌握．
练习册系列答案
阅读快车系列答案
相关题目
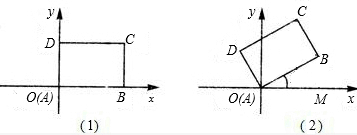
（2012•利川市一模）折纸与证明---用纸折出黄金分割点：
折纸与证明---用纸折出黄金分割点：