题目内容
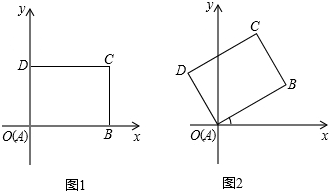
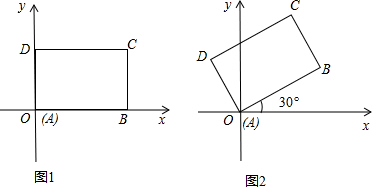
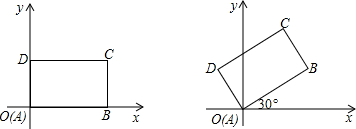
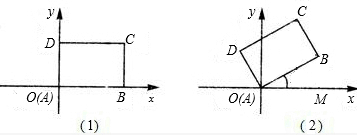
先将一矩形ABCD置于直角坐标系中,使点A与坐标系的原点重合,边AB、AD分别落在x轴、y轴上(如左图),再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图),若AB=8,BC=6,则右图中点C的坐标为 .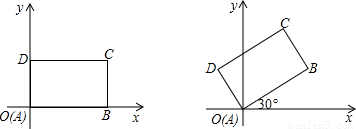
【答案】分析:延长CB交x轴于点E,则∠ABE=90°,∠AEB=60°.可求AE、BE的长度.
作CF⊥AE于F.求AF,CF的长度便知C点坐标.解直角三角形CFE可求CF、EF的长度,从而知AF的长度.问题得解.
解答:解:延长CB交x轴于点E,作CF⊥AE于F.
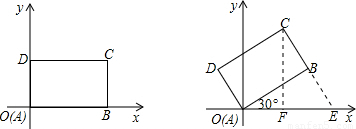
在Rt△ABE中,
∵AB=8,∠BAE=30°,
∴∠BEA=60°,BE=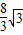 ,AE=
,AE=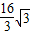 .
.
在Rt△CEF中,
CE=6+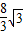 ,∠CEF=60°,
,∠CEF=60°,
∴EF=3+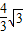 ,CF=3
,CF=3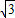 +4.
+4.
∴AF=AE-EF=4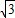 -3.
-3.
∴C(4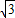 -3,3
-3,3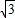 +4).
+4).
点评:此题重点考查了利用解直角三角形求点的坐标,涉及图形的旋转变换,综合性很强,难度很大.
作CF⊥AE于F.求AF,CF的长度便知C点坐标.解直角三角形CFE可求CF、EF的长度,从而知AF的长度.问题得解.
解答:解:延长CB交x轴于点E,作CF⊥AE于F.

在Rt△ABE中,
∵AB=8,∠BAE=30°,
∴∠BEA=60°,BE=
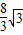 ,AE=
,AE=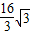 .
.在Rt△CEF中,
CE=6+
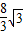 ,∠CEF=60°,
,∠CEF=60°,∴EF=3+
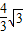 ,CF=3
,CF=3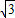 +4.
+4.∴AF=AE-EF=4
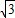 -3.
-3.∴C(4
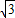 -3,3
-3,3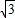 +4).
+4).点评:此题重点考查了利用解直角三角形求点的坐标,涉及图形的旋转变换,综合性很强,难度很大.

练习册系列答案
相关题目