题目内容
当x取某一范围的实数时,代数式
+
的值是一个常数,该常数是( )
| (16-x)2 |
| (x-13)2 |
| A、29 | B、16 | C、13 | D、3 |
分析:将被开方数中16-x和x-13的取值范围进行讨论.
解答:解:
+
=|16-x|+|x-13|,
(1)当
时,解得13<x<16,原式=16-x+x-13=3,为常数;
(2)当
时,解得x<13,原式=16-x+13-x=29-2x,不是常数;
(3)当
时,解得x>16;原式=x-16+x-13=2x-29,不是常数;
(4)当
时,无解.
故选D
| (16-x)2 |
| (x-13)2 |
(1)当
|
(2)当
|
(3)当
|
(4)当
|
故选D
点评:解答此题,要弄清二次根式的性质:
=|a|,分类讨论的思想.
| a2 |

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
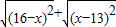 的值是一个常数,该常数是( )
的值是一个常数,该常数是( )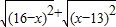 的值是一个常数,该常数是( )
的值是一个常数,该常数是( )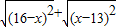 的值是一个常数,该常数是( )
的值是一个常数,该常数是( )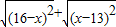 的值是一个常数,该常数是( )
的值是一个常数,该常数是( )