题目内容
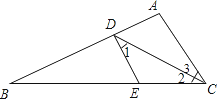
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
【答案】
(1)解:如图1,连接FO,

∵F为BC的中点,AO=CO,
∴OF∥AB,
∵AC是⊙O的直径,
∴CE⊥AE,
∵OF∥AB,
∴OF⊥CE,
∴OF所在直线垂直平分CE,
∴FC=FE,OE=OC,
∴∠FEC=∠FCE,∠0EC=∠0CE,
∵∠ACB=90°,
即:∠0CE+∠FCE=90°,
∴∠0EC+∠FEC=90°,
即:∠FEO=90°,
∴FE为⊙O的切线;
(2)解:如图2,
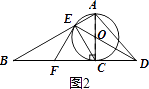
∵⊙O的半径为3,
∴AO=CO=EO=3,
∵∠EAC=60°,OA=OE,
∴△AOE是等边三角形,
∴∠EOA=60°
∴∠COD=∠EOA=60°,
∵在Rt△OCD中,∠COD=60°,OC=3,
∴CD= ![]() ,
,
∵在Rt△ACD中,∠ACD=90°,
CD= ![]() ,AC=6,
,AC=6,
∴AD= ![]() .
.
【解析】(1)由已知可知,添加辅助线连接FO,易证OF是△ABC的中位线,得到OF∥AB,又有AC是⊙O的直径,证得OF垂直平分EC。根据垂直平分线的性质及等角的余角相等得到∠FEO=90°,从而得到结论。或证△OEF和△OFC,即可得出结论。
(2)根据已知条件易证得△AOE是等边三角形,得出∠COD=∠EOA=60°,在Rt△OCD中求出CD的长,再在Rt△ACD中根据勾股定理求出AD的长即可。
【考点精析】根据题目的已知条件,利用线段垂直平分线的判定和含30度角的直角三角形的相关知识可以得到问题的答案,需要掌握和一条线段两个端点距离相等的点,在这条线段的垂直平分线上;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案