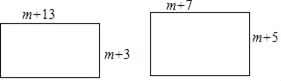
题目内容
【题目】某数学兴趣小组对线段上的动点问题进行探究,已知AB=8.
问题思考:
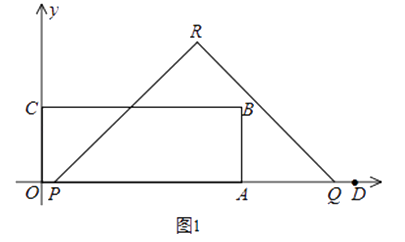
如图1,点P为线段AB上的一个动点,分别以AP、BP为边在同侧作正方形APDC、BPEF.
(1)当点P运动时,这两个正方形的面积之和是定值吗?若是,请求出;若不是,请求出这两个正方形面积之和的最小值.
(2)分别连接AD、DF、AF,AF交DP于点K,当点P运动时,在△APK、△ADK、△DFK中,是否存在两个面积始终相等的三角形?请说明理由.
问题拓展:
(3)如图2,以AB为边作正方形ABCD,动点P、Q在正方形ABCD的边上运动,且PQ=8.若点P从点A出发,沿A→B→C→D的线路,向点D运动,求点P从A到D的运动过程中,PQ的中点O所经过的路径的长.
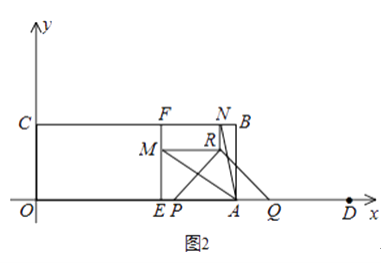
(4)如图3,在“问题思考”中,若点M、N是线段AB上的两点,且AM=BN=1,点G、H分别是边CD、EF的中点,请直接写出点P从M到N的运动过程中,GH的中点O所经过的路径的长及OM+OB的最小值.
【答案】
(1)
解:当点P运动时,这两个正方形的面积之和不是定值.
设AP=x,则PB=8﹣x,
根据题意得这两个正方形面积之和=x2+(8﹣x)2
=2x2﹣16x+64
=2(x﹣4)2+32,
所以当x=4时,这两个正方形面积之和有最小值,最小值为32.
(2)
解:存在两个面积始终相等的三角形,它们是△APK与△DFK.
依题意画出图形,如答图2所示.
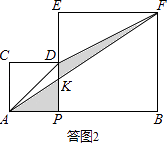
设AP=a,则PB=BF=8﹣a.
∵PE∥BF,
∴ ![]() ,即
,即 ![]() ,
,
∴PK= ![]() ,
,
∴DK=PD﹣PK=a﹣ ![]() =
= ![]() ,
,
∴S△APK= ![]() PKPA=
PKPA= ![]()
![]() a=
a= ![]() ,S△DFK=
,S△DFK= ![]() DKEF=
DKEF= ![]()
![]() (8﹣a)=
(8﹣a)= ![]() ,
,
∴S△APK=S△DFK.
(3)
解:当点P从点A出发,沿A→B→C→D的线路,向点D运动时,不妨设点Q在DA边上,
若点P在点A,点Q在点D,此时PQ的中点O即为DA边的中点;
若点Q在DA边上,且不在点D,则点P在AB上,且不在点A.
此时在Rt△APQ中,O为PQ的中点,所以AO= ![]() PQ=4.
PQ=4.
所以点O在以A为圆心,半径为4,圆心角为90°的圆弧上.
PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如答图3所示:

所以PQ的中点O所经过的路径的长为: ![]() ×2π×4=6π.
×2π×4=6π.
(4)
解:点O所经过的路径长为3,OM+OB的最小值为 ![]() .
.
如答图4﹣1,分别过点G、O、H作AB的垂线,垂足分别为点R、S、T,则四边形GRTH为梯形.
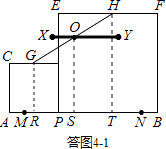
∵点O为中点,
∴OS= ![]() (GR+HT)=
(GR+HT)= ![]() (AP+PB)=4,即OS为定值.
(AP+PB)=4,即OS为定值.
∴点O的运动路径在与AB距离为4的平行线上.
∵MN=6,点P在线段MN上运动,且点O为GH中点,
∴点O的运动路径为线段XY,XY= ![]() MN=3,XY∥AB且平行线之间距离为,点X与点A、点Y与点B之间的水平距离均为2.5.
MN=3,XY∥AB且平行线之间距离为,点X与点A、点Y与点B之间的水平距离均为2.5.
如答图4﹣2,作点M关于直线XY的对称点M′,连接BM′,与XY交于点O.
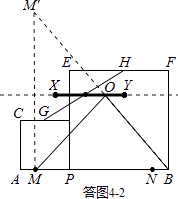
由轴对称性质可知,此时OM+OB=BM′最小.
在Rt△BMM′中,MM′=2×4=8,BM=7,由勾股定理得:BM′= ![]() =
= ![]() .
.
∴OM+OB的最小值为 ![]() .
.
【解析】(1)设AP=x,则PB=8﹣x,根据正方形的面积公式得到这两个正方形面积之和=x2+(8﹣x)2 , 配方得到2(x﹣4)2+32,然后根据二次函数的最值问题求解.(2)根据PE∥BF求得PK= ![]() ,进而求得DK=PD﹣PK=a﹣
,进而求得DK=PD﹣PK=a﹣ ![]() =
= ![]() ,然后根据面积公式即可求得.(3)本问涉及点的运动轨迹.PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如答图3所示;(4)本问涉及点的运动轨迹.GH中点O的运动路径是与AB平行且距离为3的线段XY上,如答图4﹣1所示;然后利用轴对称的性质,求出OM+OB的最小值,如答图4﹣2所示.
,然后根据面积公式即可求得.(3)本问涉及点的运动轨迹.PQ的中点O所经过的路径是三段半径为4,圆心角为90°的圆弧,如答图3所示;(4)本问涉及点的运动轨迹.GH中点O的运动路径是与AB平行且距离为3的线段XY上,如答图4﹣1所示;然后利用轴对称的性质,求出OM+OB的最小值,如答图4﹣2所示.
【考点精析】本题主要考查了二次函数的性质和正方形的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如下表:
购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?