题目内容
【题目】如图,在矩形AB CD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动;点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0<t<6).
(1)当t为何值时,△QAP为等腰直角三角形?
(2)四边形QAPC的面积与t的大小有关系吗?请说明理由.
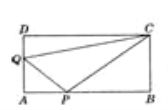
【答案】(1)t为2秒时,△QAP为等腰直角三角形;
(2)四边形QAPC的面积与t的大小没有关系
【解析】试题分析:(1)根据题意得到AP=2t,DQ=t,根据等腰直角三角形的性质列出方程,解方程即可;(2)根据四边形QAPC的面积=四边形ABCD的面积-△CDQ的面积-△PBC的面积计算;
试题解析:
(1)∵当QA=AP时,△QAP为等腰直角三角形.
∴![]() 解得:
解得: ![]() ,
,
即t为2秒时,△QAP为等腰直角三角形.
(2)四边形QAPC的面积=![]() 为常数.
为常数.
所以四边形QAPC的面积与t的大小没有关系.

练习册系列答案
相关题目

