题目内容
(2012•德化县一模)如图,在直角坐标系中,⊙O的圆心O在坐标原点,直径AB=8,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为y=x+m,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE⊥x轴交⊙O 于点E,过点E作EG⊥y轴于G,过点C作CF⊥y轴于F,连接DE.
于点E,过点E作EG⊥y轴于G,过点C作CF⊥y轴于F,连接DE.
(1)填空:∠CPB=
(2)试探究:在P点运动过程中,PD2+PC2的值是否会发生变化?若变化,请说明理由;如果不变化,请求出这个值;
(3)如果点P在射线AB上运动,当△PDE的面积为4时,请你求出CD的长度.
 于点E,过点E作EG⊥y轴于G,过点C作CF⊥y轴于F,连接DE.
于点E,过点E作EG⊥y轴于G,过点C作CF⊥y轴于F,连接DE.(1)填空:∠CPB=
45
45
°;(2)试探究:在P点运动过程中,PD2+PC2的值是否会发生变化?若变化,请说明理由;如果不变化,请求出这个值;
(3)如果点P在射线AB上运动,当△PDE的面积为4时,请你求出CD的长度.
分析:(1)利用图象与x,y轴交点坐标得出QO=PO,从而得出∠CPB的度数即可;
(2)根据PD2+PC2=PD2+PE2=DE2,得出PD2+PC2=32即可;
(3)分别从当点P在直径AB上时,以及当点P在线段AB的延长线上时得出CD与CM的长度关系,进而求出即可.
(2)根据PD2+PC2=PD2+PE2=DE2,得出PD2+PC2=32即可;
(3)分别从当点P在直径AB上时,以及当点P在线段AB的延长线上时得出CD与CM的长度关系,进而求出即可.
解答: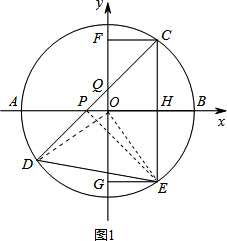 (1)解:过点P的直线PQ的解析式为y=x+m,
(1)解:过点P的直线PQ的解析式为y=x+m,
当x=0,y=m,当y=0,x=-m,
故QO=PO,
则∠CPB=45°;
故答案为:45;
(2)不变,
证明:如图1,连接PE,EO,DO,
∵AB垂直平分CE,
∴PC=PE,且∠CPB=∠EPH=45°,
∴PE⊥CD,
∴PD2+PC2=PD2+PE2=DE2,
∵∠PCH=45°,
∴
=90°,
∴DO⊥EO,
∴DE=
OD=4
,
∴PD2+PC2=32;

(3)解:当点P在直径AB上时,
S△PDE=
PD×PE=
PD×PC=4,
故PD×PC=8,
又∵PD2+PC2=32,
∴CD2=(PD+PC)2=32+16=48,
∴CD=4
,
当点P在AB延长线上,如图2,
同理可得:
CD2=(PD-PC)2=32-16=16,
解得CD=4.
综上所述,CD的长为4
或4.
 (1)解:过点P的直线PQ的解析式为y=x+m,
(1)解:过点P的直线PQ的解析式为y=x+m,当x=0,y=m,当y=0,x=-m,
故QO=PO,
则∠CPB=45°;
故答案为:45;
(2)不变,
证明:如图1,连接PE,EO,DO,
∵AB垂直平分CE,
∴PC=PE,且∠CPB=∠EPH=45°,
∴PE⊥CD,
∴PD2+PC2=PD2+PE2=DE2,
∵∠PCH=45°,
∴
 |
| DE |
∴DO⊥EO,
∴DE=
| 2 |
| 2 |
∴PD2+PC2=32;

(3)解:当点P在直径AB上时,
S△PDE=
| 1 |
| 2 |
| 1 |
| 2 |
故PD×PC=8,
又∵PD2+PC2=32,
∴CD2=(PD+PC)2=32+16=48,
∴CD=4
| 3 |
当点P在AB延长线上,如图2,
同理可得:
CD2=(PD-PC)2=32-16=16,
解得CD=4.
综上所述,CD的长为4
| 3 |
点评:此题主要考查了圆的综合题,三角形的面积以及平方差公式应用以及一次函数的综合应用,要注意的是(3)中,要根据P点的不同位置进行分类求解.

练习册系列答案
相关题目
 (2012•德化县一模)如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.
(2012•德化县一模)如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A. (2012•德化县一模)友情提示:请同学们做完上面考题后,再认真检查一遍,估计一下你的得分情况.如果你全卷得分低于90分(及格线),则本题的得分将计入全卷总分,但计入后全卷总分最多不超过90分;如果你全卷总分已经达到或超过90分,则本题的得分不计入全卷总分.
(2012•德化县一模)友情提示:请同学们做完上面考题后,再认真检查一遍,估计一下你的得分情况.如果你全卷得分低于90分(及格线),则本题的得分将计入全卷总分,但计入后全卷总分最多不超过90分;如果你全卷总分已经达到或超过90分,则本题的得分不计入全卷总分.