题目内容
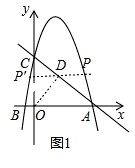
【题目】如图，抛物线y=ax2+bx+6与x轴交于点A（6，0），B（﹣1，0），与y轴交于点C．
（1）求抛物线的解析式；
（2）若点M为该抛物线对称轴上一点，当CM+BM最小时，求点M的坐标.
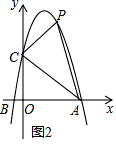
（3）抛物线上是否存在点P，使△ACP为直角三角形？若存在，有几个？写出所有符合条件的点P的坐标；若不存在，说明理由．
【答案】（1）y=﹣x2+5x+6；（2）点M（
）；（3）点P的坐标为（﹣2，﹣8）或（4，10）或（2+2
，4+2）或（2﹣2，4﹣2）．
【解析】
（1）已知C（0，6），由交点式设抛物线解析式为y=a（x+1）（x﹣6），把C点代入即可求解；
（2）先求出抛物线的对称轴，再作出点B关于抛物线对称轴的对称点（即为A点），连接AC交对称轴于点M，再求AC与对称轴的交点可得结果；
（3）由点P在抛物线上，可先设出P点坐标，然后分别表示出PC2、PA2 、AC2，再按照∠PAC=90°、∠PCA=90°、∠APC=90°三种情况分别求解即可.
（1）当x=0时，y=ax2+bx+6=6，则C（0，6），
设抛物线的解析式为y=a（x+1）（x﹣6），
把C（0，6）代入得a1（﹣6）=6，解得a=﹣1，
∴抛物线的解析式为y=﹣（x+1）（x﹣6），即y=﹣x2+5x+6；
（2）∵抛物线的对称轴是直线x=
，直线AC的解析式为y=-x+6，点B关于对称轴直线x=
的对称点为点A，
∴连接AC，交直线x=于点M，此时点M满足CM+BM最小，
当x=时，y=
，∴点M（
）
（3）设P点坐标为（x，﹣x2+5x+6），存在4个点P，使△ACP为直角三角形．
PC2=x2+（﹣x2+5x）2，PA2=（x﹣6）2+（﹣x2+5x+6）2，AC2=62+62=72，
当∠PAC=90°，∵PA2+AC2=PC2，
∴（x﹣6）2+（﹣x2+5x+6）2+72=x2+（﹣x2+5x）2，
整理得x2﹣4x﹣12=0，解得x1=6（舍去），x2=﹣2，此时P点坐标为（﹣2，﹣8）；
当∠PCA=90°，∵PC2+AC2=PA2，
72+x2+（﹣x2+5x）2=（x﹣6）2+（﹣x2+5x+6）2，
整理得x2﹣4x=0，解得x1=0（舍去），x2=4，此时P点坐标为（4，10）；
当∠APC=90°，∵PA2+AC2=PC2，
∴（x﹣6）2+（﹣x2+5x+6）2+x2+（﹣x2+5x）2=72，
整理得x3﹣10x2+20x+24=0，
x3﹣10x2+24x﹣4x+24=0，
x（x2﹣10x+24）﹣4（x﹣6）=0，
x（x﹣4）（x﹣6）﹣4（x﹣6）=0，
（x﹣6）（x2﹣4x﹣4）=0，
而x﹣6≠0，
所以x2﹣4x﹣4=0，解得x1=2+2，x2=2﹣2，此时P点坐标为（2+2，4+2）或（2﹣2，4﹣2）；
综上所述，符合条件的点P的坐标为（﹣2，﹣8）或（4，10）或（2+2，4+2）或（2﹣2，4﹣2）．
