题目内容
在Rt△ABC中,∠C=90°,AC=3,BC=4,以直线AC为轴,把△ABC旋转一周得到的圆锥的侧面积是 .
20∏
利用勾股定理易得圆锥的母线长,那么圆锥的侧面积=底面周长×母线长÷2.
解:AC=3,BC=4,由勾股定理得斜边AB=5,以直线AC为轴,把△ABC旋转一周得到的圆锥的底面半径为4,
底面周长=8π,侧面面积=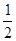 ×8π×5=20π.
×8π×5=20π.
本题利用了勾股定理,圆的周长公式和扇形面积公式求解.
解:AC=3,BC=4,由勾股定理得斜边AB=5,以直线AC为轴,把△ABC旋转一周得到的圆锥的底面半径为4,
底面周长=8π,侧面面积=
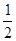 ×8π×5=20π.
×8π×5=20π.本题利用了勾股定理,圆的周长公式和扇形面积公式求解.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目


 角度得到的,若点A’在AB上,,则旋转角
角度得到的,若点A’在AB上,,则旋转角


 中,
中, ,
, ,
, .
. 与点
与点 重合,折痕与
重合,折痕与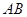 ,
, 分别
分别 和点
和点 (如图4),折痕
(如图4),折痕 的长为_________。
的长为_________。