题目内容
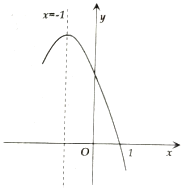
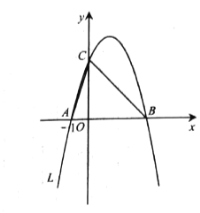
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]()
![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)![]() 与
与![]() 之间的关系式为: ;
之间的关系式为: ;
(2)判断线段![]() 和
和![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)设点![]() 是抛物线
是抛物线![]() 上
上![]() 、
、![]() 之间的动点,连接
之间的动点,连接![]() ,
,![]() ,当
,当![]() 时:
时:
①若![]() ,求点
,求点![]() 的坐标;
的坐标;
②若![]() ,且
,且![]() 的最大值为
的最大值为![]() ,请直接写出
,请直接写出![]() 的值.
的值.

【答案】(1)c﹣b= 1;(2)OB=OC,理由见解析;(3)①点P的坐标为(1,4)或(2,3);② ![]() 或
或![]()
【解析】
(1)将A(-1,0)代入抛物线![]() 即可得解;
即可得解;
(2)由抛物线![]() 可得点C的坐标,故可得OC=c,
可得点C的坐标,故可得OC=c,![]() 代入抛物线
代入抛物线![]() 得
得![]() 可得B(0,c),故可得OB=c,故可得结论;
可得B(0,c),故可得OB=c,故可得结论;
(3)①设点P(x,y),根据![]() 可得
可得![]() ,求解方程即可得到解答;
,求解方程即可得到解答;
②根据二次函数图象的增减性结合![]() 的最大值分3种情况求解即可.
的最大值分3种情况求解即可.
(1)∵抛物线![]() 经过
经过![]()
代入得:![]()
![]()
![]()
故答案为:![]() .
.
(2)OB=OC.
∵抛物线![]() 与
与![]() 轴交于点C,
轴交于点C,
![]()
![]()
由(1)知,![]() 代入抛物线
代入抛物线![]() 得,
得,
![]()
解得:![]() ,
,![]() ,
,
∵![]() ,
,
![]()
![]()
![]()
(3)① 当m=3时,得:![]() 解得:
解得:![]()
∴![]() .
.
∴OB=OC=3,
∵A(﹣1,0),
∴AB=4.
∴![]() .
.
连接OP(如图所示),则有:
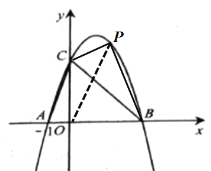
![]() .
.
∵点P(x,y)在抛物线L上,
∴![]() .
.
∴![]() ,
,
∵S△PBC=![]() S△ABC,
S△ABC,
∴![]() ,
,
即![]() ,
,
解得:x1=1,x2=2.
当x=1时,![]() ;当x=2时,
;当x=2时,![]() .
.
∴点P的坐标为(1,4)或(2,3).
②∵抛物线![]()
∴对称轴为![]()
∵图象开口向下,
![]() 时,y随x的增大而增大,
时,y随x的增大而增大,![]() 时,y随x的增大而减小,
时,y随x的增大而减小,
a.当![]() 时,即
时,即![]() 时,y最大值
时,y最大值![]()
![]() 或
或![]() (不符合题意,舍去)
(不符合题意,舍去)
b.当![]() 时,y最大值
时,y最大值![]()
![]() (不符合题意,舍去)
(不符合题意,舍去)
c.当![]() 时,y最大值
时,y最大值![]() ,
,
![]() 或
或![]() (不符合题意,舍去)
(不符合题意,舍去)
综上所述:![]() 或
或![]()

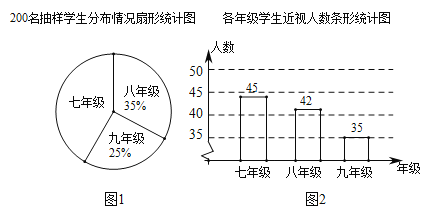
【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
运动服款式 | 甲 | 乙 |
进价(元/套) | 80 | 100 |
售价(元/套) | 120 | 160 |
若购进两种款式的运动服共300套,且投入资金不超过26800元.
(1) 该服装店应购进甲款运动服至少多少套?
(2)若服装店购进甲款运动服的进价每套降低a元,并保持这两款运动服的售价不变,且最多购进240套甲款运动服.如果这批运动服售出后,服装店刚好获利18480元,求a的取值范围.
【题目】观察下列等式,探究发现规律,并解决问题,
①![]() ;
;
②![]() ;
;
③![]() ;
;
(1)直接写出第④个等式: ;
(2)猜想第![]() 个等式(用含字母
个等式(用含字母![]() 的式子表示),并说明这个等式的正确性;
的式子表示),并说明这个等式的正确性;
(3)利用发现的规律,求![]() 的值.(参考数据:
的值.(参考数据:![]() )
)
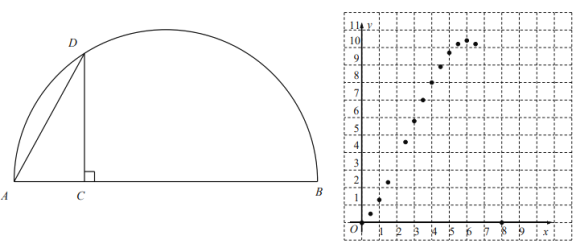
【题目】如图,![]() 是线段
是线段![]() 上--动点,以
上--动点,以![]() 为直径作半圆,过点
为直径作半圆,过点![]() 作
作![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )请根据学习函数的经验,对函数
)请根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
![]() 通过画图、测量、计算,得到了
通过画图、测量、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
补全表格中的数值: ![]() ;
;![]() ;
;![]() .
.
![]() 根据表中数值,继续描出
根据表中数值,继续描出![]() 中剩余的三个点
中剩余的三个点![]() ,画出该函数的图象并写出这个函数的一条性质;
,画出该函数的图象并写出这个函数的一条性质;
![]() 结合函数图象,直接写出当
结合函数图象,直接写出当![]() 的面积等于
的面积等于![]() 时,
时,![]() 的长度约为___ _
的长度约为___ _![]() .
.