题目内容
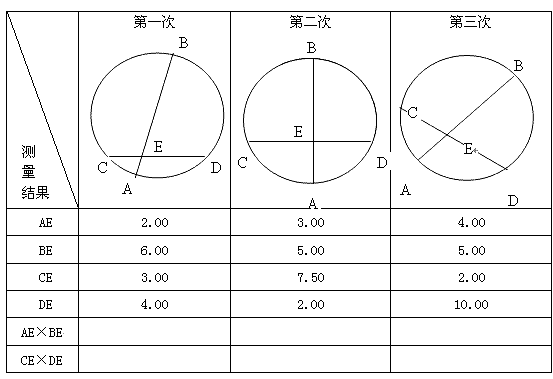
在一次数学实验探究课中,需要研究两个同心圆内有关线段的关系问题,某同学完成了以下部分记录单:记录单 (单位:cm)
| 第一次 | 第二次 | 第三次 | |
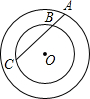
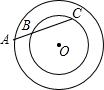
| 图形 R=5 r=3 |
 |
 |
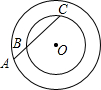 |
| AB | 2.50 | 3.00 | 3.50 |
| AC | 6.40 | 5.33 | 4.57 |
| AB•AC |
(2)对半径分别为R、r的两个同心圆,猜测AB•AC与R、r的关系式,并加以证明.
分析:(1)利用计算器进行准确计算;
(2)首先根据(1)中计算的数值,可以猜想AB•AC=R2-r2,然后进一步运用相似三角形的性质进行证明.
(2)首先根据(1)中计算的数值,可以猜想AB•AC=R2-r2,然后进一步运用相似三角形的性质进行证明.
解答: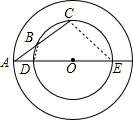 解:(1)AB•AC=2.5×6.4=16;
解:(1)AB•AC=2.5×6.4=16;
AB•AC=3.00×5.33=15.99;
AB•AC=15.995;
(2)因为R2-r2=16,所以AB•AC=R2-r2.证明如下:
过点O作直线AE,交小圆与D,E,连接BD、CE.
∵∠A=∠A,∠ABD=∠E,
∴△ABD∽△AEC.
∴
=
,
即AB•AC=AD•AE=(R+r)(R-r)=R2-r2.
 解:(1)AB•AC=2.5×6.4=16;
解:(1)AB•AC=2.5×6.4=16;AB•AC=3.00×5.33=15.99;
AB•AC=15.995;
(2)因为R2-r2=16,所以AB•AC=R2-r2.证明如下:
过点O作直线AE,交小圆与D,E,连接BD、CE.
∵∠A=∠A,∠ABD=∠E,
∴△ABD∽△AEC.
∴
| AC |
| AD |
| AE |
| AB |
即AB•AC=AD•AE=(R+r)(R-r)=R2-r2.
点评:此题考查了学生数学中的猜想探究能力,能够熟练运用相似三角形的判定和性质进行证明.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在一次数学实验探究课中,需要研究同一个圆中两条线段的关系问题,某同学完成了以下部分的记录,单位:cm
(1)请你计算 AE×BE,CE×DE的值,并填入上表相应的位置.
(2)猜想对在同一个圆中,两条线段相交,被交点分成的两条线段的积有什么关系?并试着证明.
(3)利用上述结论,解决问题:AB为⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径R.
| 测量结果 | 第一次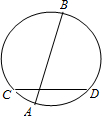 |
第二次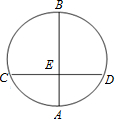 |
第三次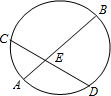 |
| AE | 2.00 | 3.00 | 2.99 |
| BE | 6.01 | 5.00 | 5.00 |
| CE | 3.01 | 3.88 | 3.75 |
| DE | 3.99 | 3.87 | 4.00 |
| AE×BE | |||
| CE×DE |
(2)猜想对在同一个圆中,两条线段相交,被交点分成的两条线段的积有什么关系?并试着证明.
(3)利用上述结论,解决问题:AB为⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径R.
在一次数学实验探究课中,需要研究两个同心圆内有关线段的关系问题,某同学完成了以下部分记录单:
记录单 (单位:cm)
| 第一次 | 第二次 | 第三次 | |
| 图形 R=5 r=3 | 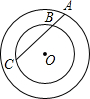 | 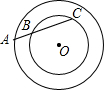 | 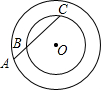 |
| AB | 2.50 | 3.00 | 3.50 |
| AC | 6.40 | 5.33 | 4.57 |
| AB•AC |
(2)对半径分别为R、r的两个同心圆,猜测AB•AC与R、r的关系式,并加以证明.
在一次数学实验探究课中,需要研究同一个圆中两条线段的关系问题,某同学完成了以下部分的记录,单位:cm
(1)请你计算 AE×BE,CE×DE的值,并填入上表相应的位置.
(2)猜想对在同一个圆中,两条线段相交,被交点分成的两条线段的积有什么关系?并试着证明.
(3)利用上述结论,解决问题:AB为⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径R.
| 测量结果 | 第一次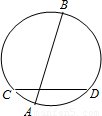 | 第二次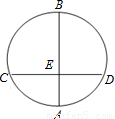 | 第三次 |
| AE | 2.00 | 3.00 | 2.99 |
| BE | 6.01 | 5.00 | 5.00 |
| CE | 3.01 | 3.88 | 3.75 |
| DE | 3.99 | 3.87 | 4.00 |
| AE×BE | |||
| CE×DE |
(2)猜想对在同一个圆中,两条线段相交,被交点分成的两条线段的积有什么关系?并试着证明.
(3)利用上述结论,解决问题:AB为⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径R.