题目内容
【题目】如图,在Rt![]() 中,∠C=90°,AC=BC,在线段CB延长线上取一点P,以AP为直角边,点P为直角顶点,在射线CB上方作等腰 Rt
中,∠C=90°,AC=BC,在线段CB延长线上取一点P,以AP为直角边,点P为直角顶点,在射线CB上方作等腰 Rt![]() , 过点D作DE⊥CB,垂足为点E.
, 过点D作DE⊥CB,垂足为点E.

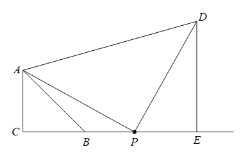
(1) 依题意补全图形;
(2) 求证: AC=PE;
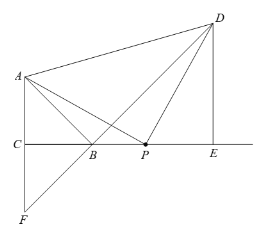
(3) 连接DB,并延长交AC的延长线于点F,用等式表示线段CF与AC的数量关系,并证明.
【答案】(1)见解析;(2)见解析;(3)AC=CF,见解析
【解析】
(1)根据描述作出图形;
(2)先证明△ACP≌△DEP,根据全等的性质即可得出结论;
(3)根据(2)中全等得出PC=DE,再由线段间的转化可得出PC=BE,故可得出△DBE为等腰直角三角形,从而△BCF也为等腰直角三角形,结论得证.
解:(1)依题意补全图形;
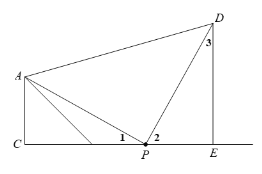
(2) 证明:∵DE⊥CB, ∠C=90°,
∴∠DEP=∠C =90°,
∴∠3+∠2=90°,
又∵∠APD =90°,
∴∠1+∠2=90°,
∴∠1=∠3,
又∵AP=DP,
∴△ACP≌△PED (AAS),
∴AC=PE.
(3) 线段CF与AC的数量关系是CF=AC.
∵△ACP≌△PED,
∴PC=DE,
又∵AC=BC,
∴BC=PE, ∴PC=BE,
∴BE=DE,
即△DBE为等腰直角三角形,
易证△BCF为等腰直角三角形,
∴BC=CF,
∴AC=CF .

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目







