题目内容
已知.如图,BC为半圆O的直径,F是半圆上异于B、C的一点,A是 | BF |
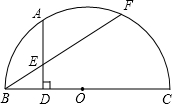 AD于点E.
AD于点E.(1)求证:BE•BF=BD•BC;
(2)试比较线段BD与AE的大小,并说明道理.
分析:(1)连接FC,根据有两组角相等的两个三角形相似得到△BDE∽△BFC,根据相似三角形的对应边成比例即可得到结论.
(2)连接AC,AB,根据圆周角定理及余角的性质可得到BE=AE,由已知可知BE>BD,从而就得到AE>BD.
(2)连接AC,AB,根据圆周角定理及余角的性质可得到BE=AE,由已知可知BE>BD,从而就得到AE>BD.
解答: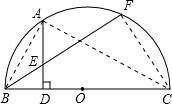 (1)证明:连接FC,∵BC为半圆O的直径
(1)证明:连接FC,∵BC为半圆O的直径
则BF⊥FC
∵∠BFC=∠BDE=90°,∠FBC=∠EBD
∴△BDE∽△BFC
∴BE:BC=BD:BF
∴BE•BF=BD•BC
(2)解:AE>BD.理由如下:
连接AC,AB,则∠BAC=90°
∵A是
的中点
∴∠ABF=∠ACB
∵∠ACB+∠ABC=90°,∠BAD+∠ABC=90°
∴∠ACB=∠BAD
∴∠BAD=∠ABF
∴BE=AE
∵BE>BD
∴AE>BD
 (1)证明:连接FC,∵BC为半圆O的直径
(1)证明:连接FC,∵BC为半圆O的直径则BF⊥FC
∵∠BFC=∠BDE=90°,∠FBC=∠EBD
∴△BDE∽△BFC
∴BE:BC=BD:BF
∴BE•BF=BD•BC
(2)解:AE>BD.理由如下:
连接AC,AB,则∠BAC=90°
∵A是
 |
| BF |
∴∠ABF=∠ACB
∵∠ACB+∠ABC=90°,∠BAD+∠ABC=90°
∴∠ACB=∠BAD
∴∠BAD=∠ABF
∴BE=AE
∵BE>BD
∴AE>BD
点评:此题主要考查学生对相似三角形的判定及圆周角定理等知识点的综合运用.

练习册系列答案
相关题目
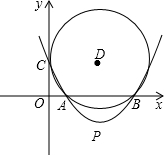 B、C三点作⊙D.若⊙D与y轴相切.
B、C三点作⊙D.若⊙D与y轴相切.
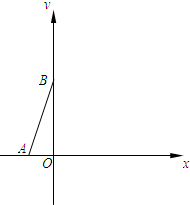 (2012•闵行区二模)已知:如图,抛物线y=-x2+bx+c与x轴的负半轴相交于点A,与y轴相交于点B(0,3),且∠OAB的余切值为
(2012•闵行区二模)已知:如图,抛物线y=-x2+bx+c与x轴的负半轴相交于点A,与y轴相交于点B(0,3),且∠OAB的余切值为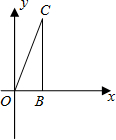 (2012•鄂州)已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=
(2012•鄂州)已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=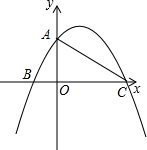 (2013•封开县一模)已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(-1,0).
(2013•封开县一模)已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(-1,0).