题目内容
已知:如图,在直角坐标系xoy中,以x轴的负半轴上一点H为圆心作⊙H与x轴交于A、B两点,与y轴交于C、D两点.以C为圆心、OC为半径作⊙C与⊙H交于F、F两点,与y轴交于O、Q两点.直线EF与AC、BC、y轴分别于M、N、G三点.直线y=| 3 | 4 |
(1)求tan∠CNM的值;
(2)连接OM、ON,问:四边形CMON是怎样的四边形?请说明理由.
(3)如图,R是⊙C中弧EQ上的一动点(不与E点重合),过R作⊙C的切线RT,若RT与⊙H相交于S、T不同两点.问:CS•CT的值是否发生变化?若不变,请说明理由,并求其值;若变化,请求其值的变化范围.

分析:(1)连接CH,则CH⊥EF,即∠CNM+∠HCB=90°.再根据题意得出∠CNM=∠CAB.由y=
x+3过A、C,从而得出tan∠CNM的值.
(2)由GD•GC=GE•GF,GO•GQ=GE•GF,得GO•GQ=GD•GC,则GO=GC.还可证得GC=GM,则GO=GC=GM=GN,从而得出四边形OMCN是矩形.
(3)连接CR,过C作⊙H的直径CL,连接SL.易证△CLS∽△CTR,即
=
,从而得出CS•CT的值不变,是定值.
| 3 |
| 4 |
(2)由GD•GC=GE•GF,GO•GQ=GE•GF,得GO•GQ=GD•GC,则GO=GC.还可证得GC=GM,则GO=GC=GM=GN,从而得出四边形OMCN是矩形.
(3)连接CR,过C作⊙H的直径CL,连接SL.易证△CLS∽△CTR,即
| CL |
| CT |
| CS |
| CR |
解答: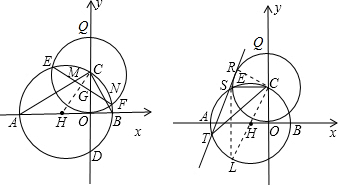 解:(1)连接CH,
解:(1)连接CH,
则CH⊥EF,即∠CNM+∠HCB=90°.
而∠HCB=∠CBA,即∠CNM+∠CBA=90°.
又∵∠CAB+∠CBA=90°,
∴∠CNM=∠CAB.
由y=
x+3过A、C,则OC=3,AO=4,
即tan∠CNM=tan∠CAB=
;
(2)由GD•GC=GE•GF,GO•GQ=GE•GF,得GO•GQ=GD•GC,
即GO(GC+CQ)=(GO+OD)•GC,则GO=GC.
又∠CMG=∠CBA=∠ACO,
即GC=GM,则GO=GC=GM=GN,
故四边形OMCN是矩形;
(3)连接CR,过C作⊙H的直径CL,连接SL.
易证△CLS∽△CTR,即
=
,
则CS•CT=CL•CR=AB•OC=(4+
)×3=
.
故CS•CT的值不变为
.
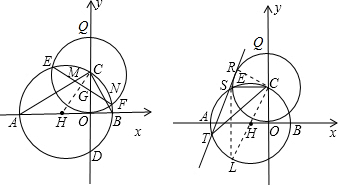 解:(1)连接CH,
解:(1)连接CH,则CH⊥EF,即∠CNM+∠HCB=90°.
而∠HCB=∠CBA,即∠CNM+∠CBA=90°.
又∵∠CAB+∠CBA=90°,
∴∠CNM=∠CAB.
由y=
| 3 |
| 4 |
即tan∠CNM=tan∠CAB=
| 3 |
| 4 |
(2)由GD•GC=GE•GF,GO•GQ=GE•GF,得GO•GQ=GD•GC,
即GO(GC+CQ)=(GO+OD)•GC,则GO=GC.
又∠CMG=∠CBA=∠ACO,
即GC=GM,则GO=GC=GM=GN,
故四边形OMCN是矩形;
(3)连接CR,过C作⊙H的直径CL,连接SL.
易证△CLS∽△CTR,即
| CL |
| CT |
| CS |
| CR |
则CS•CT=CL•CR=AB•OC=(4+
| 9 |
| 4 |
| 75 |
| 4 |
故CS•CT的值不变为
| 75 |
| 4 |
点评:本题是一道综合题,考查了相交两圆的性质、圆内接四边形的性质、相似三角形的判定和性质等知识点,是中考压轴题,难度较大.注:(1)利用了等角代换来求三角函数的值,这是在圆中常碰到的事.
(2)充分运用几何图形的性质模索出MN与OC相等且互相平分,从而正确地判断图形.
(3)通过相似三角形,硬性求出CS•CT的值,这是处理这类问题的又一方法.
(2)充分运用几何图形的性质模索出MN与OC相等且互相平分,从而正确地判断图形.
(3)通过相似三角形,硬性求出CS•CT的值,这是处理这类问题的又一方法.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目

 的图象的一个分支位于第一象限.
的图象的一个分支位于第一象限.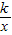 的图象的图象上,求k的值;
的图象的图象上,求k的值; S1?
S1?
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
