��Ŀ����
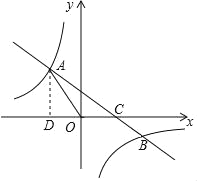
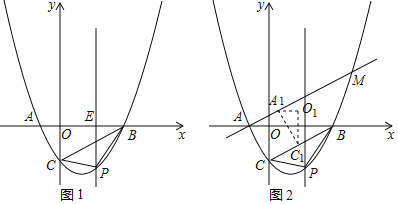
����Ŀ����ƽ��ֱ������ϵxOy�У���֪������y=x2-bx+5��x�ύ��A��B���㣬��y�ύ�ڵ�C����֪��A�������ǣ�1��0������A�ڵ�B�����.
��1���������ߵĺ�������ʽ��
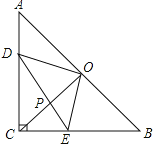
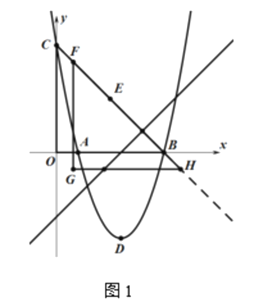
��2����ͼ1����EΪBC���е㣬����BOC��CE�������ƽ�ƣ�ƽ�ƺ�õ���������Ϊ��HGF������F���E�غ�ʱֹͣ�˶�.��ƽ�Ƶľ���CF=m������HGF��ֱ��l��y=x-3�·���ͼ�����ΪS����S����m�ĺ�������ʽ��
��3����ͼ2������AC��BC����M��E�ֱ���AC, BC���е�.��P���߶�ME����һ�㣬��Q���߶�AB����һ��.�ֽ�����������������
��һ������������CAB����λ��ME��ֽƬ���������֣������߶�ME������ȡһ��P���߶�AB������ȡһ��Q����PQ���ı���ֽƬMABE���������֣�
�ڶ�������PQ���ֽƬ��M�㰴˳ʱ�뷽����ת180����ʹ�߶�MA��MC�غϣ���PQ�Ҳ�ֽƬ��E�㰴��ʱ�뷽����ת180����ʹ�߶�EC��EB�غϣ�ƴ��һ����������ֽƬABC�����ȵ��ı���ֽƬ��(ע���ü���ƴͼ���̾����Ҳ��ص�)
��ƴ�ɵ�����ı���ֽƬ���ܳ�����Сֵ�����ֵ�ĺ�.
���𰸡���1��y=x2-6x+5����2��S =![]() ����3������ܳ�����С�ܳ��ĺ���
����3������ܳ�����С�ܳ��ĺ���![]() .
.
��������
��1�����ô���ϵ������⼴�ɣ�
��2�����з������ۣ��ٵ�0��m��![]() ʱ�������J�����꣬�������JHK��������ɣ��ڵ�
ʱ�������J�����꣬�������JHK��������ɣ��ڵ�![]() ��m��
��m��![]() ʱ�������FJK�������������ı���KGHJ��������ɣ�
ʱ�������FJK�������������ı���KGHJ��������ɣ�
��3��ͨ��ƴͼ�����������ܳ�����С�ܳ�.
��1������֪������y=x2-bx+5��x�ύ��A��1��0�����������ʽ����0=12-m+5��
��ã�b=6.
�������߽���ʽΪy=x2-6x+5.
��2����ͼ��
�ٵ�0��m��![]() ʱ�������ֱ�߽���J�������
ʱ�������ֱ�߽���J�������![]() ��
��![]()
��J���������(4��1).
��CJ=4��BJ=![]() ��
��
��JH=![]() +m.
+m.
��S=��JHK�����=![]()
�ڵ�![]() ��m��
��m��![]() ʱ��
ʱ��
��BH=CF=m,BJ=![]() ��
��
��JH=![]() +m.
+m.
��FJ=![]() -JH=
-JH=![]()
����FJK�������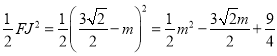
S=�ı���KGHJ�����=![]() ��
��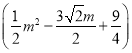 =
=![]() .
.
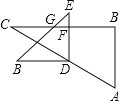
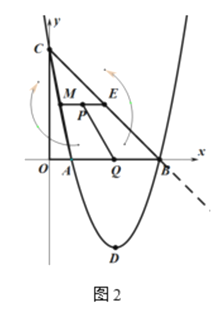
��3��ƴ�ɵ��ı��α���ƽ���ı��Σ���ͼ��ʾʱ�ܳ���С����ʱƴ�ɵ�ͼ���Ǿ���.PQ��AB�������A(1��0)��B(5��0)��AB=4.ME=2.
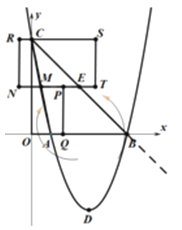
��NT=4��RN=PQ=![]()
����С�ܳ�=2����4+![]() ��=13.
��=13.
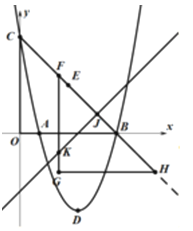
��ͼ����ʾʱ���ܳ����.��ʱ��NT=4��RM=MB=![]()

������ܳ�![]()
������ܳ�����С�ܳ��ĺ���![]() .
.

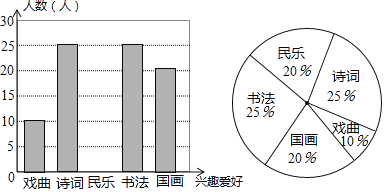
����Ŀ��ѧУ��֯��Уʫ�ʴ�ᡱ��ȫУѧ���μӳ�����Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ�˲���ѧ���ijɼ�������100�֣��������õ����²�������ͳ��ͼ����
��� | �ɼ�x�� | Ƶ���������� | Ƶ�� |
��1�� | 50��x��60 | 6 | 0.12 |
��2�� | 60��x��70 | 0.16 | |
��3�� | 70��x��80 | 14 | a |
��4�� | 80��x��90 | b | |
��5�� | 90��x��100 | 10 |
�����ͼ�������ṩ����Ϣ�ش��������⣺
��1��ͳ�Ʊ���a���� ��b���� ��
��2���뽫ͳ��ͼ������������
��3�����ݵ�����������Ƹ�У1200��ѧ���У��ɼ�������80�ֵ�������